\(\sqrt[3]{x-6}\) chuyển sang pascal là gì?

Những câu hỏi liên quan
\(\sqrt[3]{x-6}\) chuyển sang pascal là gì ?
Biểu thức Pascal: (a+cos(x))/sqrt(sqr(a)+sqr(x)+1) khi chuyển sang toán học có dạng:
Đọc tiếp
Biểu thức Pascal: (a+cos(x))/sqrt(sqr(a)+sqr(x)+1) khi chuyển sang toán học có dạng:
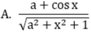
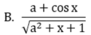

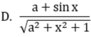
Chuyển biểu thức toán học sang pascal và ngược lại
a) \(\dfrac{1}{2n}\)≤\(\dfrac{3}{5}\)\(\cos\)2π
b)\(\dfrac{\sqrt{x^2+y^{3x}}}{a-\dfrac{a}{b}}z-\dfrac{1}{2}\)
c) Sqrt(a+2/(sqrt(2+a))-(x/a*b)
d) abs(x-2*y)+sqr(x*x)-2*cos(x)
d: \(=\left|x-2y\right|+\left(x\cdot x\right)^2-2\cdot cos\left(x\right)\)
Đúng 1
Bình luận (0)
Biểu thức Pascal B: = Sqr(sqrt(x1-x2)+sqrt(y1-y2)) khi chuyển sang toán học có dạng:
![]()
![]()
![]()
![]()
Chuyển pascal sang toán học :
a) 3* sqr(a)+abs(b)
b) 12/5*sqrt(x)-sqrt(y)
Trong đó : + sqr : bình phương
+ abs : trị tuyệt đối
+ sqrt : \(\sqrt{2}\)
a, 3.a2+ |b|
b, \(\frac{12}{5}\)\(\sqrt{x}\) -\(\sqrt{y}\)
c,
Đúng 0
Bình luận (0)
mong các bạn chỉ cho mình với , mai mình có bài kiểm tra 1 tiết .
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Viết chương trình con chuyển các từ viết thường sang viết hoa. (trong pascal)
Vd: pascal sang PASCAL
Program Doi_Sang_Chu_Hoa;
Var S , SH: String; i : Byte;
Begin
Write('Nhap vao mot chuoi chu thuong : '); Readln(S);
SH := ''; {tạo xâu rỗng SH}
For i := 1 to Length(S) do SH[i] := UpCase(S[i];
Write('Chuoi da doi sang chu hoa: ',SH);
Readln;
End.
bạn dùng hàm UpCase(kí tự) để đổi từ chữ thường sang chữ hoa
Đúng 0
Bình luận (1)
Program Chuoi_In_Hoa;
Uses Crt;
Var i:integer;st:string;
Begin
Clrscr;
Writeln(‘DOI CHUOI SANG CHUOI HOA’);
Write(‘Nhap ho ten:’);readln(st); st[1]:=upcase(st[1]);
For i:=1 to length(St) do
If st[i]=’ ‘ then st[i+1]:=upcase(st[i+1]); Writeln(‘Ho ten sau khi doi lan 1 la: ‘,st);
For i:=1 to length(St) do st[i]:=upcase(st[i]);
Writeln(‘Ho ten sau khi doi lan 2 la: ‘,st);
Readln;
End.
Đúng 0
Bình luận (1)
program helo;
ues crt;
var s:string;i:longint
begin
clrscr;
write('s:=');readln(s);
for i:=1 to length(s) do s[i]:=upcase(s[i]);
writeln('s sau khi duoc doi sang chu hoa la');
readln;
end.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chuyển biểu thức mở ngoặc (b + 5)(1-c) sang kí hiệu trong pascal là
Chuyển biểu thức đuọc viết bằng pascal sang biểu thức toán học:
((A+b+c)*2)-((a-b)*x)/y
TK
a) (a*a*a+b*x-8)/2 = (a^3 + bx - 8) : 2
Đúng 0
Bình luận (0)
a) Chuyển biểu thức được viết trong Pascal sang biểu thức toán học:
1+1/(x*x)+1/(y*y)+1/(2*2)
Xem chi tiết
\(1+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{2^2}\)
Đúng 1
Bình luận (0)
\(1+\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{2^2}\)
Đúng 1
Bình luận (0)























