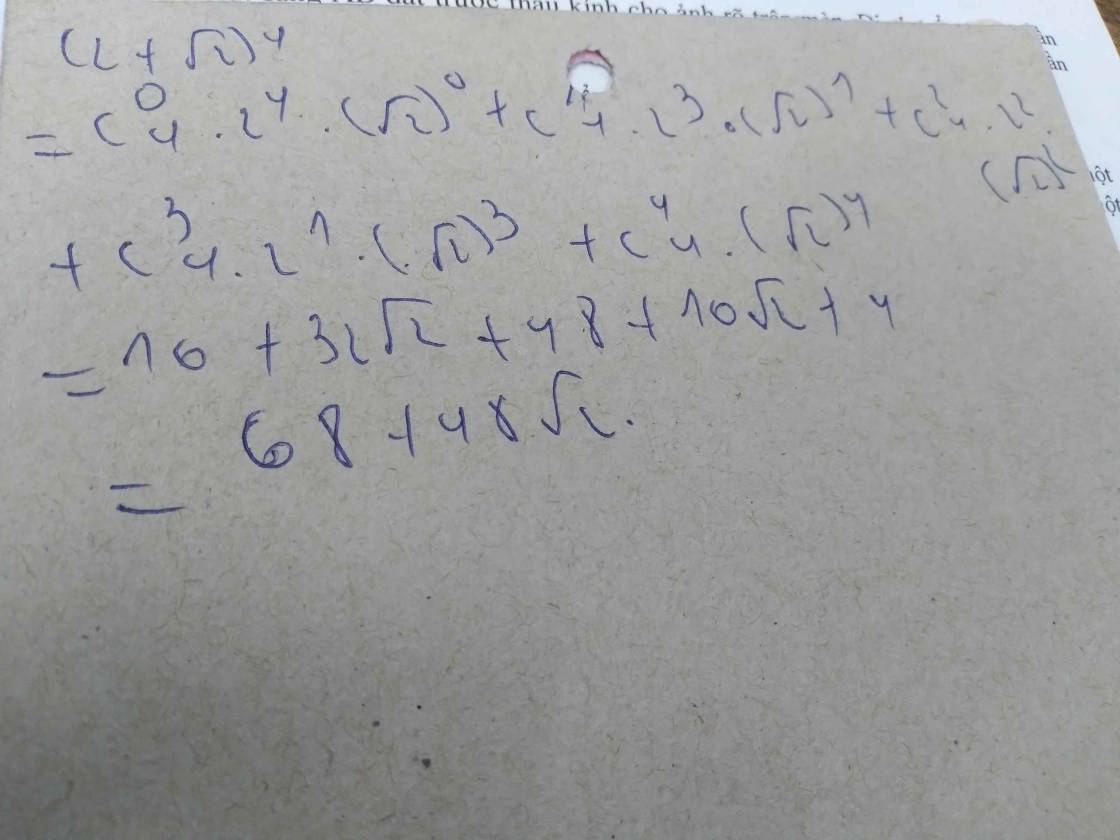khai căn biểu thức sau √(8 - 2√15)

Những câu hỏi liên quan
Chuyển các biểu thức lấy căn thành bình phương của một nhị thức rồi khai căn:
1.\(\sqrt{8+2\sqrt{15}}\)
2.\(\sqrt{15-2\sqrt{14}}\)
3.\(\sqrt{21+8\sqrt{5}}\)
1, \(\sqrt{8+2\sqrt{15}}=\sqrt{8+2\sqrt{5.3}}=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
2, \(\sqrt{15-2\sqrt{14}}=\sqrt{14-2\sqrt{14}+1}=\sqrt{\left(\sqrt{14}-1\right)^2}=\sqrt{14}-1\)
3, \(\sqrt{21+8\sqrt{5}}=\sqrt{21+2.4\sqrt{5}}=\sqrt{16+2.4\sqrt{5}+5}\)
\(=\sqrt{\left(4+\sqrt{5}\right)^2}=4+\sqrt{5}\)
khai căn biểu thức sau \(\sqrt{14-8\sqrt{3}}\)
\(=\sqrt{8+2\sqrt{8\cdot6}+6}\)
\(=\sqrt{\left(2\sqrt{2}+\sqrt{6}\right)^2}=2\sqrt{2}+6\)
Đúng 0
Bình luận (1)
Rút gọn biểu thức chứa số và căn bậc hai của căn bậc hai
căn bậc hai của 8- 2 căn 15 + căn bậc hai của9 - 4 căn 5
\(=\sqrt{5}-\sqrt{3}+\sqrt{5}-2=2\sqrt{5}-2-\sqrt{3}\)
Đúng 0
Bình luận (0)
khai triển và rút gọn biểu thức A = (2+ căn 2)^4
Rút gọn biểu thức
a, 3 căn 18 - căn 32 +4 căn 2 +căn 162
b, 2 căn 48 - 4 căn 27+ căn 75 + căn 12
c, căn 21+8 căn 5 + căn 21 -8 căn 5
d,(căn 14 - căn 7/căn 2-1 + căn 15 - căn 5/ căn 3-1 )÷1/căn 7- căn 5
a: \(=9\sqrt{2}-4\sqrt{2}+4\sqrt{2}+9\sqrt{2}=18\sqrt{2}\)
b: \(=8\sqrt{3}-12\sqrt{3}+5\sqrt{3}+2\sqrt{3}=3\sqrt{3}\)
c: \(=2\sqrt{21}\)
Đúng 0
Bình luận (0)
rút gọn biểu thức sau
a) căn 72 - căn 16/3 +4,5× căn 8/3 +2×căn27
(15 căn x-11/x+2 căn x -3) + ( 3 căn x -2/1- căn x) - ( 2 căn x +3/ căn x +3)
a. rút gọn biểu thức
b. tìm giá trị lớn nhất của biểu thức và giá trị của x tương ứng
Bài1: Rút gọn biểu thức A, A= ( căn 2/3 + căn 50/3 - căn 24) . căn 6 B, B= căn 14 - căn 7 / căn 2-1 + căn 15 - căn 5 / căn 3 -1 ) : 1/ căn 7 - căn 5 b, So sánh A và B Bài 2: Giải các phương trình sau a, căn 3x -5 căn 12x + 7 căn 27x =12 b, x / 1+ căn 1+x -1
Câu1 cho 2 biểu thức A=2 căn x/3+căn x và B=[15-căn x/x-25 +2/căn x+5]: căn x+3/căn x-5