Cho A= {x∈R/ x3-3mx2+3mx-1=0}.Tìm m để A có 3 phần tử
Tìm m để đồ thị hàm số y = x 3 - 3 m x 2 + 3 m x - 1 cắt trục Ox tại 3 điểm phân biệt có hoành độ x 1 ; x 2 ; x 3 thỏa điều kiện x 1 2 + x 2 2 + x 3 2 > 15
A. m ∈ - ∞ ; - 1 3 ∪ 1 ; + ∞
B. m ∈ - ∞ ; - 1 ∪ 1 ; + ∞
C. m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
D. m ∈ - ∞ ; - 1 3 ∪ 5 3 ; + ∞
Hoành độ giao điểm của (C) và Ox là nghiệm phương trình
x - 1 x 2 - 3 m - 1 x + 1 = 0 ⇔ x = 1 g x = x 2 - 3 m - 1 x + 1 = 0 1
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt thì (1) có 2 nghiệm phân biệt khác 1.
Khi đó ∆ > 0 g 1 ≠ 0
⇔ m > 1 m < - 1 3 m ≠ 1 ⇔ m > 1 m < - 1 3
Giả sử x 3 = 1
Theo đề thì phương trình (1) có hai nghiệm x 1 ; x 2
x 1 2 + x 2 2 > 14 ⇔ x 1 + x 2 2 - 2 x 1 x 2 > 14 ⇔ m > 5 3 m < - 1
(thỏa mãn)
Vậy m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
Đáp án C
Tìm m để hàm số y = x 3 - 3 m x 2 + 3 ( 2 m - 1 ) x + 1 đồng biến trên R
A. m = 1
B. Luôn thỏa mãn với mọi m
C. Không có giá trị m thỏa mãn
D. m ≠ 1
Đáp án A
Phương pháp giải:
Dựa vào điều kiện để hàm số đồng biến hoặc nghịch biến trên khoảng xác định
Lời giải:
Ta có
y
=
x
3
-
3
m
x
2
+
3
(
2
m
-
1
)
x
+
1
![]() R
R
Hàm số đồng biến trên R ![]() R
R ![]() R
R
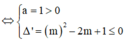
![]()
Cho hàm số y=x3-3mx2+3.(m2-1)x-m3+4m-1. Tìm m để hàm số có CĐ, CT tại 2 điểm A, B và tam giác OAB vuông tại O (gợi ý \(\overrightarrow{OA}.\overrightarrow{OB}=0\) )
Gọi x1,x2 là nghiệm của phương trình : x2-3mx+3m-2=0 (1) (m là tham số) . đạt giá trị nhỏ nhất. Tìm m để A=x12 - 3mx2-m+1
-mình sửa đề luôn nhé
\(\Delta=9m^2-4\left(3m-2\right)=9m^2-12m+8=\left(3m-2\right)^2+4>0\)
Vậy pt luôn có 2 nghiệm pb
Vì x1 là nghiệm pt trên nên
\(A=3mx_1-3m+2+3mx_2-m+1=3m.3m-4m+3\)
\(=9m^2-4m+3=9m^2-\dfrac{2.3m.4}{6}+\dfrac{16}{36}-\dfrac{16}{36}+3\)
\(=\left(3m-\dfrac{4}{6}\right)^2+\dfrac{23}{9}\ge\dfrac{23}{9}\)Dấu ''='' xảy ra khi m = 2/9
Tìm điều kiện của m để hàm số y = x3 - 3mx2 + 3(m + 2)x đồng biến trên R.
![]()
![]()
A=x^3 +3mx^2-3x-3m+2=0.Tìm m để A=x1^2+x2^2+x3^2 đạt GTNN
mình đang cần gấp lắm ạ.Mong bạn tốt bụng,dễ thương,đẹp trai,xinh gái giúp đỡ mình ạ.Cảm ơn vì đã quan tâm
Tính tổng S tất cả các giá trị của tham số m để hàm số f ( x ) = x 3 - 3 m x 2 + 3 m x + m 2 - 2 m 3 tiếp xúc với trục Ox.
A. 4 3
B. 1
C. 0
D. 2 3
Tính: tổng S tất cả các giá trị tham số m để đồ thị hàm số f ( x ) = x 3 - 3 m x 2 + 3 m x + m 2 - 2 m 3 tiếp xúc với trục hoành.
A. S = 1
B. S = 0
C. S = 2 3
D. S = 4 3
Cho hàm số y= x3- 3mx2+4m2-2 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có hai điểm cực trị A; B sao cho I( 1; 0) là trung điểm của đoạn thẳng AB.
A. 0
B. -1.
C. 1.
D. 2.
Ta có 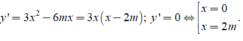
Đề đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó tọa độ hai điểm cực trị là A( 0 ; 4m2- 2) và B( 2m; 4m2- 4m3-2).
Do I( 1; 0) là trung điểm của AB nên
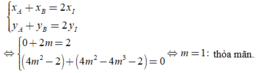
Chọn C.