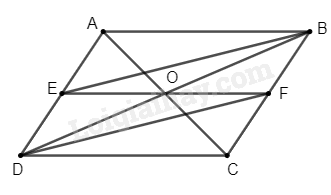
Cho hình bình hành ABCD có AD=1/2 BC, gọi E;F lần lượt là trung điểm của AB và CD.
a) AEFD và AECF là hình gì? Vì sao?
b) Chứng minh ED // FB
c) Gọi M;N là giao điểm của À với DE và BF với CF. Chứng minh EMFN là hình chữ nhật
d) Hình bình hành ABCD cần có thêm điều kiện gì để EMFN là hình vuông?