Cho x+y=2. Tìm GTLN của biểu thức B=x2y2(x2+y2)

Những câu hỏi liên quan
Cho x, y là các số thực dương thỏa mãn
2
(
x
2
+
y
2
)
+
x
y
(
x
+
y
)
(
x
y
+
2
)
Giá trị nhỏ nhất của biểu thức
P
4
(
x
3
y
3...
Đọc tiếp
Cho x, y là các số thực dương thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( x y + 2 ) Giá trị nhỏ nhất của biểu thức P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 )
A. - 25 4
B. 5
C. -13
D. - 23 4
Đáp án D
Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0 (*)
Đặt x + y = u x y = v ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0 gải ra ta được u = v + 2 + v 2 + 28 v + 4 4
Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18 , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18 ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0 với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 ) trong đó t 0 = m i n t = m i n ( x y + y x ) với x,y thỏa mãn điều kiện (*).
Ta có :
t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2
Vậy m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4
Đúng 0
Bình luận (0)
cho 2 số dương x;y thỏa mãn x2 + y2 = 1, tìm GTLN của biểu thức :
\(P=\dfrac{2xy+1}{x+y+1}\)
Ta có \(x^2+y^2=1\Leftrightarrow\left(x+y\right)^2=2xy+1\)
Từ đó \(P=\dfrac{\left(x+y\right)^2}{x+y+1}\). Đặt \(x+y=t\left(t\ge0\right)\). Vì \(x+y\le\sqrt{2\left(x^2+y^2\right)}=2\) nên \(t\le\sqrt{2}\). ĐTXR \(\Leftrightarrow x=y=\dfrac{1}{\sqrt{2}}\). Ta cần tìm GTLN của \(P\left(t\right)=\dfrac{t^2}{t+1}\) với \(0\le t\le\sqrt{2}\).
Giả sử có \(0\le t_1\le t_2\le\sqrt{2}\). Ta có BDT luôn đúng \(\left(t_2-t_1\right)\left(t_2+t_1+t_2t_1\right)\ge0\) \(\Leftrightarrow t_2^2-t_1^2+t_2^2t_1-t_2t_1^2\ge0\) \(\Leftrightarrow t_1^2\left(t_2+1\right)\le t_2^2\left(t_1+1\right)\) \(\Leftrightarrow\dfrac{t_1^2}{t_1+1}\le\dfrac{t_2^2}{t_2+1}\) \(\Leftrightarrow P\left(t_1\right)\le P\left(t_2\right)\). Như vậy với \(0\le t_1\le t_2\le\sqrt{2}\) thì \(P\left(t_1\right)\le P\left(t_2\right)\). Do đó P là hàm đồng biến. Vậy GTLN của P đạt được khi \(t=\sqrt{2}\) hay \(x=y=\dfrac{1}{\sqrt{2}}\), khi đó \(P=2\sqrt{2}-2\)
Đúng 3
Bình luận (0)
Lời giải:
$P=\frac{2xy+1}{x+y+1}=\frac{2xy+x^2+y^2}{x+y+1}=\frac{(x+y)^2}{x+y+1}$
$=\frac{a^2}{a+1}$ với $x+y=a$
Áp dụng BĐT AM-GM:
$1=x^2+y^2\geq \frac{(x+y)^2}{2}=\frac{a^2}{2}$
$\Rightarrow a^2\leq 2\Rightarrow a\leq \sqrt{2}$
$P=\frac{a^2}{a+1}=\frac{a}{1+\frac{1}{a}}$
Vì $a\leq \sqrt{2}\Rightarrow 1+\frac{1}{a}\geq 1+\frac{1}{\sqrt{2}}=\frac{2+\sqrt{2}}{2}$
$\Rightarrow P\leq \frac{\sqrt{2}}{\frac{2+\sqrt{2}}{2}}=-2+2\sqrt{2}$
Vậy $P_{\max}=-2+2\sqrt{2}$ khi $x=y=\frac{1}{\sqrt{2}}$
Đúng 1
Bình luận (0)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
Cho x, y là hai số thực khác 0. Tìm giá trị nhỏ nhất của biểu thức: M
4
x
2
y
2
x
2
+
y
2...
Đọc tiếp
Cho x, y là hai số thực khác 0. Tìm giá trị nhỏ nhất của biểu thức: M = 4 x 2 y 2 x 2 + y 2 + x 2 y 2 + y 2 x 2
Biến đổi M, ta được
M = 4 x 2 y 2 x 2 + y 2 + x 2 y 2 + y 2 x 2 = 4 x y + y x 2 + x y 2 + y x 2
Đặt a = x y ; b = y x ta được ab = 1, suy ra a 2 + b 2 ≥ 2
Từ đó ta có
M = 4 a + b 2 + a 2 + b 2 = 4 a 2 + b 2 + 2 + a 2 + b 2 + 2 4 + 3 a 2 + b 2 + 2 4 - 2 ≥ 2 + 3 – 2 = 3
Dấu "=" xảy ra <=> a = b = ±1 <=> 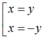
Đúng 0
Bình luận (0)
Cho các đa thức
A=x2-2y+xy+1
B=x2+y-x2y2-1
Tìm đa thức C sao cho:
C-x2+1-y=A-B ( giải bằng 3 cách)
x2 và y2 là x bình phương và y bình phương nhe các bạn!
Mình đg cần gấp ạ! Tks!
Bài 2 Phân tích đa thức sau thành nhân tử a. x4 + 2x3 − 4x − 4 b. x2(1 − x2) − 4 − 4x2 c. x2 + y2 − x2y2 + xy − x − y d* a3 + b3 + c3 − 3abc
Đọc tiếp
Bài 2 Phân tích đa thức sau thành nhân tử
a. x4 + 2x3 − 4x − 4
b. x2(1 − x2) − 4 − 4x2
c. x2 + y2 − x2y2 + xy − x − y
d* a3 + b3 + c3 − 3abc
a) \(x^4+2x^3-4x-4=\left(x^4+2x^3+x^2\right)-\left(x^2+4x+4\right)\)
\(=\left(x^2+x\right)^2-\left(x+2\right)^2=\left(x^2+x-x-2\right)\left(x^2+x+x+2\right)\)
\(=\left(x^2-2\right)\left(x^2+2x+2\right)\)
Đúng 1
Bình luận (0)
a) Ta có: \(x^4+2x^3-4x-4\)
\(=\left(x^4+2x^3+x^2\right)-\left(x^2+4x+4\right)\)
\(=\left(x^2+x\right)^2-\left(x+2\right)^2\)
\(=\left(x^2+x-x-2\right)\left(x^2+x+x+2\right)\)
\(=\left(x^2-2\right)\cdot\left(x^2+2x+2\right)\)
Đúng 0
Bình luận (0)
d) Ta có: \(a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho biểu thức P=2x-2xy-2x2-y2.Tìm GTLN của biểu thức P, khi P= GTLN thì x, y bằng mấy
Ta có: \(P=2x-2xy-2x^2-y^2\)
\(P=-x^2-2xy-y^2-x^2+2x\)
\(P=-\left(x^2+2xy+y^2\right)-\left(x^2-2x+1\right)+1\)
\(P=-\left(x+y\right)^2-\left(x-1\right)^2+1\)
\(P=-\left[\left(x+y\right)^2+\left(x-1\right)^2\right]+1\le1\forall x;y\)
Vậy GTLN của P là 1 khi x=-1; y=1.
Đúng 0
Bình luận (0)
cho (P): y = -x^2 và đường thẳng (d): y=2x+m-1
tìm m để (d) cắt (P) tại 2 điểm phân biệt A(x1;x2),B(x2;y2) mà x1y1 -x2y2 -x1x2 = 4
Trả lời:
Phương trình hoành độ giao điểm (P) và (d) ta có:
\(-x^2=2x+m-1\)
\(\Leftrightarrow x^2+2x+m-1=0\)(1)
Ta có: \(\Delta=2^2-4.1.\left(m-1\right)\)
\(=4-4m+4\)
\(=8-4m\)
Để phương trình (1) có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow8-4m>0\)
\(\Leftrightarrow4m< 8\)
\(\Leftrightarrow m< 2\)
\(\Rightarrow\)Phương trình (1) có 2 nghiệm phân biệt
\(\Rightarrow\)(d) cắt (P) tại 2 diểm phân biệt \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
Áp dụng Vi-ét \(\hept{\begin{cases}x_1+x_2=-2\left(1\right)\\x_1.x_2=m-1\left(2\right)\end{cases}}\)
Ta có \(y_1=-x_1^2\); \(y_2=-x_2^2\)
Theo đề bài:
\(x_1.y_1-x_2.y_2-x_1.x_2=4\)
\(\Leftrightarrow x_1.\left(-x_1^2\right)-x_2.\left(-x_2^2\right)-x_1.x_2=4\)
\(\Leftrightarrow-x_1^3+x_2^3-x_1.x_2=4\)
\(\Leftrightarrow-\left(x_1^3-x_2^3\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(x_1^2+x_1.x_2+x_2^2\right)-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right)\left[\left(x_1+x_2\right)^2-2x_1.x_2+x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(x_1+x_2\right)^2-x_1.x_2\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left[\left(-2\right)^2-m+1\right]-\left(m-1\right)=4\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(4-m+1\right)=4+m-1\)
\(\Leftrightarrow-\left(x_1-x_2\right).\left(3-m\right)=m+3\)
\(\Leftrightarrow-\left(x_1-x_2\right)=\frac{m+3}{3-m}\)
\(\Leftrightarrow x_1-x_2=\frac{m+3}{m-3}\)(3)
Từ (1) (3) ta có: \(\hept{\begin{cases}x_1+x_2=-2\\x_1-x_2=\frac{m+3}{m-3}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x_1=-2+\frac{m+3}{m-3}=\frac{9-m}{m-3}=-\left(m+3\right)\\x_1+x_2=-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=\frac{-\left(m+3\right)}{2}\\x_2=\frac{m-1}{2}\end{cases}}\)
Thay x1, x2 vào (2) ta có
\(x_1.x_2=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}.\frac{m-1}{2}=m-1\)
\(\Leftrightarrow\frac{-\left(m+3\right)}{2}=2\)
\(\Leftrightarrow-\left(m+3\right)=4\)
\(\Leftrightarrow m+3=-4\)
\(\Leftrightarrow m=-7\)(TM)
Vậy \(m=-7\) thì thỏa mãn bài toán
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)





















