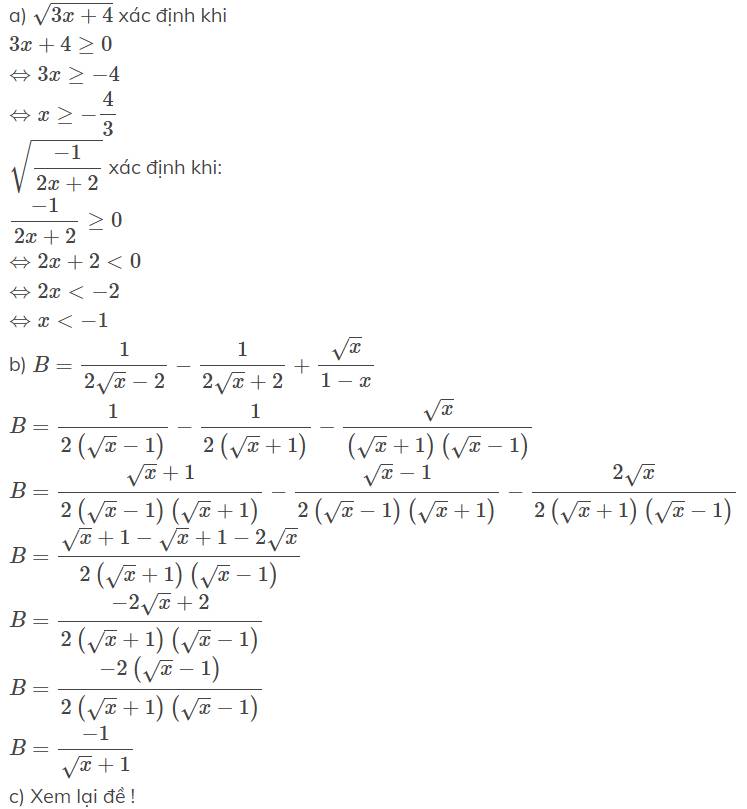Rút gọn biểu thức sau đây: \(\dfrac{a\sqrt{a}+b\sqrt{b}}{2\sqrt{a}+2\sqrt{b}}\)

Những câu hỏi liên quan
Rút gọn các biểu thức sau : a) sqrt{18left(sqrt{2}-sqrt{3}right)^2} - sqrt{54}b) dfrac{a+sqrt{ab}}{sqrt{a}-sqrt{b}} - asqrt{dfrac{1}{a}}c) ( sqrt{28} - 2sqrt{3} +7) sqrt{7} +sqrt{84}
Đọc tiếp
Rút gọn các biểu thức sau :
a) \(\sqrt{18\left(\sqrt{2}-\sqrt{3}\right)^2}\) - \(\sqrt{54}\)
b) \(\dfrac{a+\sqrt{ab}}{\sqrt{a}-\sqrt{b}}\) - a\(\sqrt{\dfrac{1}{a}}\)
c) ( \(\sqrt{28}\) - 2\(\sqrt{3}\) +7) \(\sqrt{7}\) +\(\sqrt{84}\)
a: \(=3\sqrt{2}\left(\sqrt{3}-\sqrt{2}\right)-3\sqrt{6}\)
=3căn 6-6-3căn 6=-6
b: \(=\dfrac{a+\sqrt{ab}}{\sqrt{a}-\sqrt{b}}-\sqrt{a}\)
\(=\dfrac{a+\sqrt{ab}-a+\sqrt{ab}}{\sqrt{a}-\sqrt{b}}=\dfrac{2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}\)
Đúng 1
Bình luận (0)
Rút gọn các biểu thức sau :
a) A= \(\sqrt{18}\) . \(\sqrt{2}\) - \(\sqrt{48}\) : \(\sqrt{3}\)
b)B= \(\dfrac{8}{\sqrt{5}-1}\) + \(\dfrac{8}{\sqrt{5}+1}\)
a) \(A=\sqrt{18}.\sqrt{2}-\sqrt{48}:\sqrt{3}=\sqrt{18.2}-\sqrt{48:3}\)
\(=\sqrt{36}-\sqrt{16}=6-4=2\)
b) \(B=\dfrac{8}{\sqrt{5}-1}+\dfrac{8}{\sqrt{5}+1}=\dfrac{8\sqrt{5}+8+8\sqrt{5}-8}{\left(\sqrt{5}-1\right).\left(\sqrt{5}+1\right)}=\dfrac{16\sqrt{5}}{4}=4\sqrt{5}\)
Đúng 0
Bình luận (0)
Bài 1.Rút gọn A sqrt{x^2+dfrac{2x^2}{3}} với x0Bài 2.Rút gọn biểu thức left(dfrac{10+2sqrt{10}}{sqrt{5}+sqrt{2}}+dfrac{sqrt{30}-sqrt{6}}{sqrt{5}-1}right):dfrac{2}{2sqrt{5}-sqrt{6}}Bài 3.Cho ba biểu thức A asqrt{b} + bsqrt{a};B asqrt{a}-bsqrt{b} ;C a-b.Trong ba biểu thức trên biểu thức bằng biểu thức left(sqrt{a}-sqrt{b}right)left(sqrt{a}+sqrt{b}right) với a,b0Bài 7.Cho B dfrac{1}{sqrt{1}+sqrt{2}}+dfrac{1}{sqrt{2}+sqrt{3}}+dfrac{1}{sqrt{3}+sqrt{4}}+...+dfrac{1}{sqrt{98}+sqrt{99}}+dfrac{1}{sq...
Đọc tiếp
Bài 1.Rút gọn A = \(\sqrt{x^2+\dfrac{2x^2}{3}}\) với x<0
Bài 2.Rút gọn biểu thức \(\left(\dfrac{10+2\sqrt{10}}{\sqrt{5}+\sqrt{2}}+\dfrac{\sqrt{30}-\sqrt{6}}{\sqrt{5}-1}\right)\):\(\dfrac{2}{2\sqrt{5}-\sqrt{6}}\)
Bài 3.Cho ba biểu thức A = a\(\sqrt{b}\) + b\(\sqrt{a}\);B = \(a\sqrt{a}-b\sqrt{b}\) ;C = a-b.Trong ba biểu thức trên biểu thức bằng biểu thức \(\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)\) với a,b>0
Bài 7.Cho B = \(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{98}+\sqrt{99}}+\dfrac{1}{\sqrt{99}+\sqrt{100}}\).Giá trị của biểu thức B là
Bài 8.Gọi M là giá trị nhỏ nhất của \(\dfrac{\sqrt{x}+1}{\sqrt{x}+4}\) và N là giá trị lớn nhất của \(\dfrac{\sqrt{x}+5}{\sqrt{x}+2}\).Tìm M và N
Giúp mình với!Mình đang cần gấp
1:
\(A=\sqrt{x^2+\dfrac{2x^2}{3}}=\sqrt{\dfrac{5x^2}{3}}=\left|\sqrt{\dfrac{5}{3}}x\right|=-x\sqrt{\dfrac{5}{3}}\)
2: \(=\left(\dfrac{\sqrt{100}+\sqrt{40}}{\sqrt{5}+\sqrt{2}}+\sqrt{6}\right)\cdot\dfrac{2\sqrt{5}-\sqrt{6}}{2}\)
\(=\dfrac{\left(2\sqrt{5}+\sqrt{6}\right)\left(2\sqrt{5}-\sqrt{6}\right)}{2}\)
\(=\dfrac{20-6}{2}=7\)
Đúng 0
Bình luận (0)
a) Với giá trị nào của x thì các biểu thức sau đây xác định :sqrt{3x+4} sqrt{dfrac{-1}{2x+2}}b) Rút gọn biểu thức B dfrac{1}{2sqrt{x}-2}-dfrac{1}{2sqrt{x}+2}+dfrac{sqrt{x}}{1-x} với x ≥ 0 , x ≠ 1c) Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyênD dfrac{2sqrt{x-1}}{sqrt{x}+3}
Đọc tiếp
a) Với giá trị nào của x thì các biểu thức sau đây xác định :
\(\sqrt{3x+4}\) \(\sqrt{\dfrac{-1}{2x+2}}\)
b) Rút gọn biểu thức B = \(\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\) với x ≥ 0 , x ≠ 1
c) Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên
D = \(\dfrac{2\sqrt{x-1}}{\sqrt{x}+3}\)
thực hiện phép tính ( rút gọn biểu thức )
a) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{\sqrt{a}+\sqrt{b}}{a-b}\)
b) \(\dfrac{a-b}{\sqrt{a}+\sqrt{b}}-\dfrac{a-2\sqrt{ab}+b}{\sqrt{a}-\sqrt{b}}\)
a: \(=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}\)
\(=\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)=a-b\)
b: \(=\dfrac{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}}-\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}\)
\(=\sqrt{a}-\sqrt{b}-\sqrt{a}+\sqrt{b}\)
=0
Đúng 0
Bình luận (0)
rút gọn các biểu thức sau: (giả thiết các biểu thức chữ đều có nghĩa)
a) \(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}\)
b) \(\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\)
c) \(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}\)
\(a,=\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}=\sqrt{2}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}=-\sqrt{5}\\ c,=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{2}\)
Đúng 2
Bình luận (0)
Rút gọn các biểu thức sau:
a) $A=\dfrac{\sqrt{7}-5}{2}-\dfrac{6-2 \sqrt{7}}{4}+\dfrac{6}{\sqrt{7}-2}-\dfrac{5}{4+\sqrt{7}}$;
b) $B=\dfrac{2}{\sqrt{6}-2}+\dfrac{2}{\sqrt{6}+2}+\dfrac{5}{\sqrt{6}}$.
, \(A=\frac{\sqrt{7}-5}{2}-\frac{6-2\sqrt{7}}{4}+\frac{6}{\sqrt{7}-2}-\frac{5}{4+\sqrt{7}}\)
\(=\frac{2\sqrt{7}-10-6+2\sqrt{7}}{4}+\frac{6\left(\sqrt{7}+2\right)}{3}-\frac{5\left(4-\sqrt{7}\right)}{9}\)
\(=\frac{-16+4\sqrt{7}}{4}+\frac{18\sqrt{7}+36-20+5\sqrt{7}}{9}=-4+\sqrt{7}+\frac{23\sqrt{7}+16}{9}\)
b,\(B=\frac{2}{\sqrt{6}-2}+\frac{2}{\sqrt{6}+2}+\frac{5}{\sqrt{6}}=\frac{2\left(\sqrt{6}+2\right)+2\left(\sqrt{6}-2\right)}{2}+\frac{5\sqrt{6}}{6}\)
\(=\frac{12\sqrt{6}+5\sqrt{6}}{6}=\frac{17\sqrt{6}}{6}\)
a,32 căn 7 -20/9
b, 17 căn 6 / 6
Đúng 0
Bình luận (0)
Rút gọn biểu thức sau
\(a.\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}\)
\(b.\dfrac{\sqrt{\dfrac{5}{3}}+\sqrt{\dfrac{3}{5}}-2}{\sqrt{\dfrac{5}{3}}-\sqrt{\dfrac{3}{5}}}\)
a: \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}\)
\(=\dfrac{\sqrt{2}+\sqrt{3}+2}{\sqrt{2}+\sqrt{3}+2+2+\sqrt{6}+\sqrt{8}}\)
\(=\dfrac{1}{\sqrt{2}+1}=\sqrt{2}-1\)
Đúng 2
Bình luận (0)
rút gọn các biểu thức sau: (giả thiết các biểu thức chữ đều có nghĩa)
a) \(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}\)
b) \(\dfrac{p-2\sqrt{p}}{\sqrt{p}-2}\)
làm chi tiết hộ em ạ
\(a,=\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}=-\sqrt{a}\\ b,=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)
Đúng 0
Bình luận (0)
a: \(=-\sqrt{a}\)
b: \(=\sqrt{p}\)
Đúng 0
Bình luận (0)