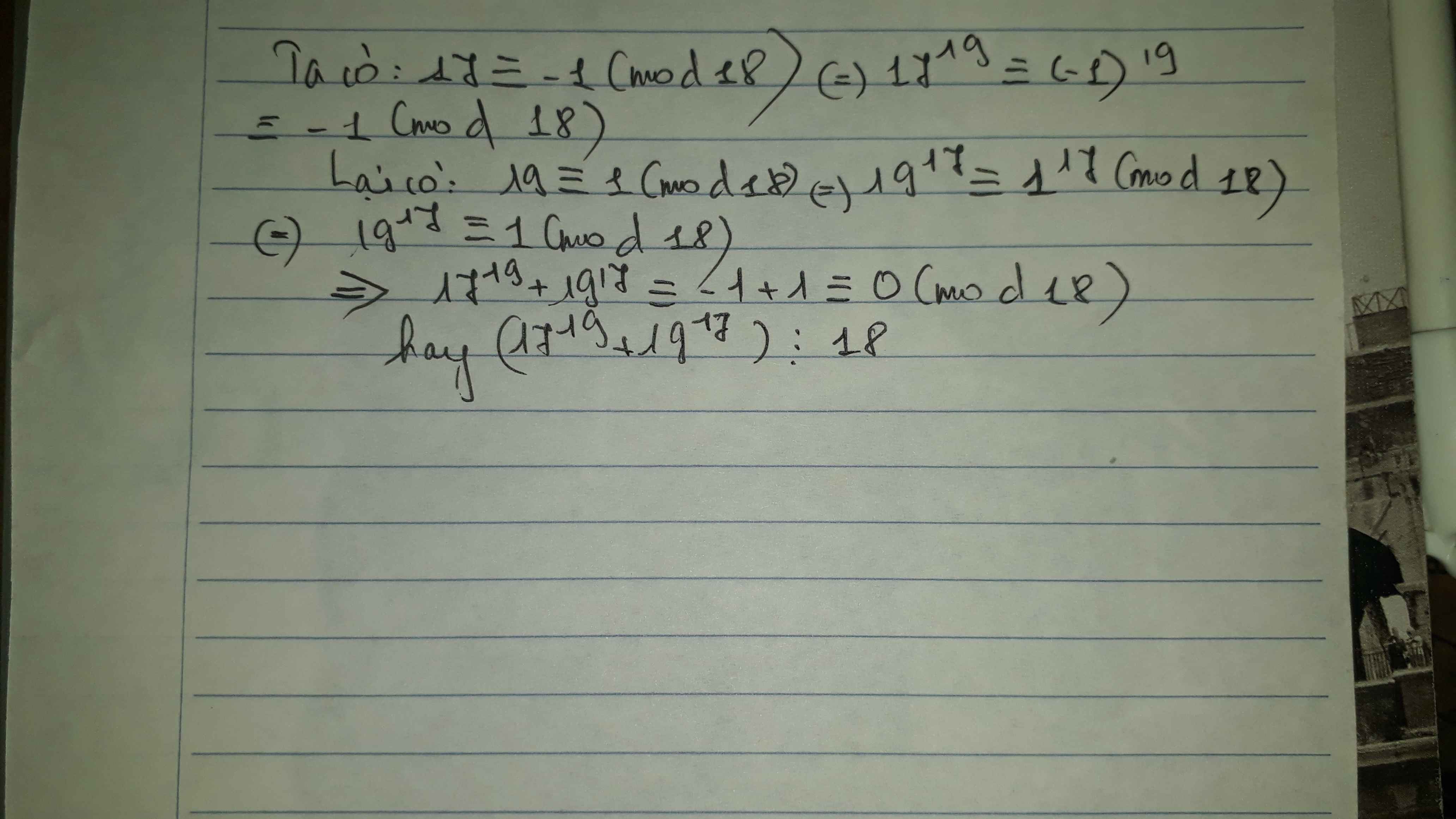Ta có: \(17^{19}+19^{17}=\left(17^{19}+1\right)+\left(19^{17}-1\right)\)

Mà \(17^{19}+1\)chia hết cho \(17+1=18\)

và \(19^{17}-1\)chia hết cho \(19-1=18\)

nên  \(\left(17^{19}+1\right)+\left(19^{17}-1\right)\)chia hết cho  \(18\)

Do đó, \(17^{19}+19^{17}\)chia hết cho  \(18\)

b) Ta có: 2^70+3^70= 4^35+9^35 chia hết cho 4+9=13

đpcm

c) 17^19 + 19^17 = (17^19 + 1) + (19^17
- 1) 
17^19 + 1 chia hết cho 17 + 1 = 18 và 19^17
- 1 chia hết cho 19 - 1 = 18 nên (17^19 + 1) + (19^17
- 1) 
hay 17^19 + 19^17 chia hết cho 18

a) Ta áp dụng đẳng thức sau: \(a^{2k+1}+b^{2k+1}⋮a+b\)

\(A=2^{70}+b^{70}=4^{35}+9^{35}⋮4+9=13\)

\(\Rightarrowđpcm\)

b) Ta có: \(17\equiv-1\left(mod18\right)\Rightarrow17^{19}\equiv-1\left(mod18\right)\)

\(19\equiv1\left(mod18\right)\Rightarrow19^{17}\equiv1\left(mod18\right)\)

\(\Rightarrow17^{19}+19^{17}⋮18\left(đpcm\right)\)

 Ta có: 

 7^17 +17.3 -1 = 7^17 +50 chia hết cho 9 
Mà 50 chia 9 dư 5 
=> 7^17 chia 9 dư 4 
=> 7^17 .7 chia 9 dư 1 
<=> 7^18 chia 9 dư 1 
18.3 -1 = 53 chia 9 dư 8 
=> 7^18 +18.3 -1 chia hết cho 9 

a) Có: \(2^3=8\equiv1\left(mod7\right)\Rightarrow2^{51}\equiv1\left(mod7\right)\)

\(\Rightarrow2^{51}-1⋮7\left(đpcm\right)\)

b) 2⁷⁰ + 3⁷⁰ = (2²)³⁵ + (3²)³⁵ = 4³⁵ + 9³⁵

\(=\left(4+9\right).\left(4^{34}-4^{33}.9+....-4.9^{33}+9^{34}\right)\)

\(=13.\left(4^{34}-4^{33}.9+...-4.9^{33}+9^{34}\right)⋮13\left(đpcm\right)\)