Cho 1 tứ giác PSRQ , có S=65 độ , R = 95 độ . Tính P, Q , gọi P, Q là x

Những câu hỏi liên quan
Cho 1 hình bình hành PSRQ
Tìm P và Q ( tìm X) trong đó R=95 độ ,
S=65 độ .
Theo tính chất hình bình hành ta luôn có hai góc đối diện luôn bằng nhau .
Do đó : \(\widehat{P}=\widehat{R}=95^0\) và \(\widehat{Q}=\widehat{S}=65^0\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD
AB//CD, Góc C = 65 độ, góc D = 95 độ, tính góc A và góc B
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
A + 950 = 1800
A = 1800 - 950
A = 850
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
B + 650 = 1800
B = 1800 - 650
B = 1150
Đúng 0
Bình luận (0)
Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD có độ dài bằng 6cm thành ba đoạn thắng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL. Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS.
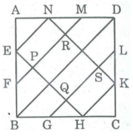
Diện tích hình vuông ABCD bằng 6.6 = 36 ( c m 2 )
Diện tích △ BEH bằng 1/2 .4.4 = 8 ( c m 2 )
Diện tích △ DKN bằng 1/2 .4.4 = 8 ( c m 2 )
Diện tích phần còn lại là: 36 - (8 + 8) = 20 ( c m 2 )
Trong tam giác vuông AEN, ta có:
E N 2 = A N 2 + A E 2 = 4 + 4 = 8 ⇒ EN = 2 2 (cm)
Trong tam giác vuông BHE, ta có:
E H 2 = B E 2 + B H 2 = 16 + 16 = 32 ⇒ EH = 4 2 (cm)
Diện tích hình chữ nhật ENKH bằng: 2 2 . 4 2 = 16 ( c m 2 )
Nối đường chéo BD. Theo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH được chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 c m 2
Diện tích △ AEN bằng 1/2 .2.2 = 2 ( c m 2 )
Vậy S A E P S N = S A E N + S E P S N = 2 + 16/4 = 6 ( c m 2 )
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có cạnh huyền bằng 12cm. Gọi E,K lần lượt là trung điểm của AB, AC
a) Tính EK
b) Gọi Q là trung điểm của BC. Chứng minh tứ giác AEQK là hình chữ nhật
c) Chọn điểm S sao cho góc ASQ = 90 độ ( S khác E và K). Tính góc ESK
Cho tứ giác ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, AC, CD, DB.
1. Chứng minh tứ giác PQRS là hình bình hành.

1) Ta có:
• PQ là đường trung bình của ΔABC nên PQ // BC và PQ = BC/2 (1)
• RS là đường trung bình của ΔDBC nên RS // BC và RS = BC/2 (2)
Từ (1) và (2) suy ra PQ // RS và PQ = RS
Suy ra tứ giác PQRS là hình bình hành.
Đúng 0
Bình luận (0)
Cho tam giác ABC gọi P và Q là chân các đường vuông góc từ đỉnh A đến các phân giác trong và ngoài của góc B .Cho R,S là chân các đường vuông góc vẽ từ A đến các đường pân giác trong và ngoài của góc Ca)Tứ giác APBQ;ARCS là hình gì ?b)CM:4 điểm P ,Q ,R ,S thẳng hàngc)CM: độ dài đoạn thẳng QS bằng nửa chu vi của tam giác ABCd)Tìm điều kiện cho tam giác ABC để tứ giác APBQ là hình vuông ?
Đọc tiếp
Cho tam giác ABC gọi P và Q là chân các đường vuông góc từ đỉnh A đến các phân giác trong và ngoài của góc B .Cho R,S là chân các đường vuông góc vẽ từ A đến các đường pân giác trong và ngoài của góc C
a)Tứ giác APBQ;ARCS là hình gì ?
b)CM:4 điểm P ,Q ,R ,S thẳng hàng
c)CM: độ dài đoạn thẳng QS bằng nửa chu vi của tam giác ABC
d)Tìm điều kiện cho tam giác ABC để tứ giác APBQ là hình vuông ?
Cho mặt cầu (S) có bán kính R cố định. Gọi (H) là hình chóp tứ giác đều có thể tích lớn nhất nội tiếp trong (S). Tìm theo R độ dài cạnh đáy (H). A.
4
R
3
B.
2
R
3
C.
R
3
D. R
Đọc tiếp
Cho mặt cầu (S) có bán kính R cố định. Gọi (H) là hình chóp tứ giác đều có thể tích lớn nhất nội tiếp trong (S). Tìm theo R độ dài cạnh đáy (H).
A. 4 R 3
B. 2 R 3
C. R 3
D. R
Cho mặt cầu (S) có bán kính R cố định. Gọi (H) là hình chóp tứ giác đều có thể tích lớn nhất nội tiếp trong (S). Tìm theo R độ dài cạnh đáy (H).
A. 4 R 3
B. 2 R 3
C. R 3
D.R
Đáp án A

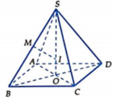
Ký hiệu như hình vẽ. Đặt A B = B C = C D = D A = a ; S O = h
Suy ra S B = a 2 2 + h 2
Gọi M là trung điểm của SB
Trong (SBD) kẻ trung trực của SB cắt SO tại I
Vậy I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD. Suy ra I S = R .
Hai tam giác vuông SMI và SOB đồng dạng ⇒ S I S B = S M S O ⇒ R = a 2 + 2 h 2 4 h với 0 < h < 2 R . Suy ra a 2 = 2 h 2 R − h .
Thể tích V của khối chóp là:
V = 1 3 a 2 h = 1 3 2 h 2 2 R − h = 8 3 h 2 h 2 2 R − h ≤ 8 3 h 2 + h 2 + 2 R − h 3 3 = 64 R 3 81
Vậy GTLN của V bằng 64 R 3 81 đạt được khi h 2 = 2 R − h ⇔ h = 4 R 3
Suy ra a = 4 R 3 .
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có . Gọi M, N, P, Q theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.a. Tính số đo góc D.b. Chứng minh tứ giác MNPQ là hình bình hành.c. Biết đường chéo BD 22cm. Tính độ dài đoạn thẳng MQ.
Đọc tiếp
Cho tứ giác ABCD có . Gọi M, N, P, Q theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.
a. Tính số đo góc D.
b. Chứng minh tứ giác MNPQ là hình bình hành.
c. Biết đường chéo BD = 22cm. Tính độ dài đoạn thẳng MQ.
b: Xét ΔABC có
M là trung điểm của BA
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành
Đúng 0
Bình luận (0)