Theo tính chất hình bình hành ta luôn có hai góc đối diện luôn bằng nhau .
Do đó : \(\widehat{P}=\widehat{R}=95^0\) và \(\widehat{Q}=\widehat{S}=65^0\)
Cho 1 tứ giác PSRQ , có S=65 độ , R = 95 độ . Tính P, Q , gọi P, Q là x
Hình bình hành ABCD có góc C<90 độ. Chứng minh rằng: \(AD^2=CD^2-CA^2-2CD.CD.cos\widehat{ACD}\)
Một hình bình hành có hai cạnh là 10 cm và 12cm góc tạo bởi hai cạnh đó bằng 150°.Diện tích của hình bình hành ấy là: A.40√3 B.60 C.60√3 D.30√3
a) vẽ đồ thị hàm số sau trên cùng mặt phẳng toạ độ Oxy
(d): y = x - 2
(d’): y = - 2x + 1
b) tìm toạ độ giao điểm E của 2 đường thẳng (d) và (d')
c) hãy tìm m để đồ thị hàm số y= (m-2)x+m và 2 đường thẳng (d),(d') đồng qui
Bài 1: Tính các độ dài x, y trong hình bên: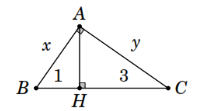
Bài 2: Giải \(\Delta\)ABC vuông tại A, biết AB = 3,5 và AC = 4,2.
1. Tìm tọa độ giao điểm 2 đường thẳng: y = 3x + 2 và y = 2x - 3
2. Tìm m để 3 đường thẳng y = 3x + 2 ; y = 2x - 3; y = (m - 2)x + 3 - m đồng quy
1 Tam giác đều có độ dài cạnh bằng 3cm. Tính diện tích tam giác.
2. Tam giác cân có cạnh bên bằng 8, cạnh đáy bằng 6. Tính diện tích tam giác.
3.Một hình thang có một đáy là 2x và các cạnh còn lại bằng x. Tìm x biết diện tích
hình thang bằng 6 căn 3 .
4.Một người đi xe đạp từ C đến Bvới vận tốc 15km/h. Hỏi đi được bao lâu thì người
đó cách đều hai điểm A và B?
5. Bạn Rô muốn treo một banner khuyến mãi dài 7m trước cửa hiệu. Có hai đinh treo
được đóng trên tường, tạo thành một đoạn thẳng song song mặt đất và có độ dài 10m.
Nếu muốn banner treo thấp hơn đoạn thẳng đó 1m thì độ dài hai dây treo phải là bao
nhiêu?
bài 2 Tisnhg ía trị biểu thức:
a) sin230 độ - sin240 độ - sin250 độ + sin2 60 độ
b) cos225 độ - cos235độ + cos245 độ -cos2 55 độ + cos2 65 độ
Bài 1: Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH và AH = 12 cm ; BC = 25 cm.
a) 
Tìm độ dài của BH; CH; AB và AC.
b) Vẽ trung tuyến AM. Tính AM
c) Tìm diện tích của rAHM.
Bài 2: Cho tam giác DEF vuông tại D, đường cao DH. Biết DE = 12 cm; EF = 20. Tính DF; EH; FH.
Bài 3: Cho tam giác DEF vuông tại D, đường cao DH. Biết EH = 1 cm; FH = 4 cm. Tính EF; DE; DF.
Bài 4: BP 2017-2018
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4cm, CH = 9cm.
a) Tính độ dài đường cao AH và ABC của tam giác ABC.
b) Vẽ đường trung tuyến AM, (M e BC) của tam giác ABC. Tính AM và diện tích của tam giác
Bài 5. Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 3 và 4 . Hãy tính các cạnh góc vuông của tam giác vuông này, đường trung tuyến ứng với cạnh huyền và diện tích tam giác ABC
Bài 6. (1.0 điểm)
Cho tam giác ABC vuông tại A, có AB = 15cm và AC = 20cm. Tính độ dài đường cao AH và trung tuyến AM của tam giác ABC.
