a: Thay x=5/2 và y=-5 vào f(x), ta được:

5/2m=-5

=>m=-2

c: \(\overrightarrow{OA}=\left(1;-2\right)\)

\(\overrightarrow{OB}=\left(2;1\right)\)

Vì 1/2<>-2/1

nên O,A,B ko thẳng hàng

1C

2A

3C

4B

cái gì thế này???????????????????????????????????

mik lp 6 nhưng nhìn bài của bn mik ko hiểu j cả luôn ý

Ta có: \(\frac{a}{b}=\frac{c}{d}\)

Áp dụng t/c của dãy tỉ số = nhau, ta có:

\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)

=> \(\frac{a}{b}=\frac{a+c}{b+d}\)(đpcm)

Vậy\(\frac{a}{b}=\frac{a+c}{b+d}\)

a) Đặt a/b=c/d=k(k thuộc Q)

    Suy ra a=b.k

          c=d.k

    Ta có :a+c/b+d=b.k+dk/d+b=k.(b+d)/b+d=k

    a/b=bk/b=k(2)

    c/d=dk/d=k(3)

     Từ (1);(2);(3) suy ra a/b=c/d

b) Ta có:x/5=y/3=x+y/5+3=16/8=2

    x/5=2 suy ra x=10

    y/3=2 suy ra y=6

a)Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{a}{b}=\frac{c}{d}=\frac{a-c}{b-d}=\frac{a+\left(-c\right)}{b+\left(-d\right)}\)

Vậy ta có điều phải chứng minh

b)Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{x}{5}=\frac{y}{3}=\frac{x+y}{5+3}=\frac{16}{8}=2\)

=>x=2.5=10

    y=2.3=6

Vậy x=10 và y=6

b) theo đề ta có: \(\frac{x}{5}=\frac{y}{3}\) và x + y = 16

áp dụng t/c DTSBN ta có:

\(\frac{x}{5}=\frac{y}{3}=\frac{x+y}{5+3}=\frac{16}{8}=2\)

=> \(\frac{x}{5}=2=>x=10\)

\(\frac{y}{3}=2=>y=6\)

vậy x = 10 ; y = 6

chúc bn hok tốt!!

573578769870678567362345215345645654654657657566876894637537

1a) \(0,31:0,91=x:\frac{49}{3}\)

=> \(\frac{0,31}{0,91}=\frac{3x}{49}\)

=> \(3x=\frac{3}{7}.49\)

=> \(3x=21\)

=> \(x=21:3=7\)

b) \(6,88:x=12:27\)

=> \(\frac{6,88}{x}=\frac{12}{27}\)

=> \(x=6,88:\frac{4}{9}\)

=> \(x=15,48\)

c) \(\frac{25}{3}:\frac{35}{3}=13:2x\)

=> \(\frac{13}{2x}=\frac{5}{7}\)

=> \(2x=13:\frac{5}{7}\)

=> \(2x=\frac{91}{5}\)

=> \(x=\frac{91}{5}:2=\frac{91}{10}\)

d) \(\left(x-1\right):24,5=5:8,75\)

=> \(\frac{x-1}{24,5}=\frac{5}{8,75}\)

=> \(x-1=\frac{4}{7}.24,5\)

=> \(x-1=14\)

=> \(x=14+1=15\)

2a) Ta có: \(\frac{x}{y}=\frac{5}{7}\) => \(\frac{x}{5}=\frac{y}{7}\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

   \(\frac{x}{5}=\frac{y}{7}=\frac{x+y}{5+7}=\frac{4,08}{12}=0,34\)

=> \(\hept{\begin{cases}\frac{x}{5}=0,34\\\frac{y}{7}=0,34\end{cases}}\) => \(\hept{\begin{cases}x=0,34.5=1,7\\y=0,34.7=2,38\end{cases}}\)

Vậy x = 1,7; y = 2,38

b) Ta có: \(\frac{x}{y}=-\frac{3}{7}\) => \(\frac{x}{-3}=\frac{y}{7}\)

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:

  \(\frac{x}{-3}=\frac{y}{7}=\frac{x-y}{-3-7}=\frac{-40}{-10}=4\)

=> \(\hept{\begin{cases}\frac{x}{-3}=4\\\frac{y}{7}=4\end{cases}}\) => \(\hept{\begin{cases}x=4.\left(-3\right)=-12\\y=4.7=28\end{cases}}\)

vậy x = -12; y = 28

c) Ta có: \(\frac{x}{y}=\frac{3}{5}\) => \(\frac{x}{3}=\frac{y}{5}\)

Đặt : \(\frac{x}{3}=\frac{y}{5}=k\) => \(\hept{\begin{cases}x=3k\\y=5k\end{cases}}\) (*)

Khi đó, ta có: xy = 1215

hay 3k. 5k = 1215

=> 15k² = 1215

=> k² = 1215 : 15 = 81

=> k = \(\pm\)9 

Thay k = \(\pm\)9 vào (*), ta được:

+) x = 3. (\(\pm\)9) = \(\pm\)27

+) y = 5. (\(\pm\)9) = \(\pm\)45

Vậy ...

Mơn bn nhiều <3

1. a) Để hàm số đồng biến thì m-1>0\(\Rightarrow\)m>1  b) Để hàm số nghịch biến m-1<0\(\Rightarrow\)m<1        2. a) Tự làm  b) Xét phương trình hoành độ -2x+1=2x\(\Rightarrow\)x=1/4\(\Rightarrow\)   y=1/2. Vậy giao điểm của d và d' có tọa độ (1/4; 1/2)              

3 a)ĐKXĐ \(x\ge0\)\(x\ne1\)A=\(\frac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)=\(\frac{-2}{\sqrt{x}+1}\)  b)Khi x= \(6-2\sqrt{5}\)thì A=\(\frac{-2}{\sqrt{\left(\sqrt{5}-1\right)^2}+1}\)=\(\frac{2}{\sqrt{5}}\)

Lời giải:

** Sửa lại hàm số: $y=-x+3$

a. Bạn có thể tự vẽ.

b. Để $y=(2k-1)x+1$ song song với (d)$ thì:

$2k-1=-1$

$\Leftrightarrow k=0$

c. PT hoành độ giao điểm của $(d)$ và $y=(k-3)x+5$:

$-x+3=(k-3)x+5$

$\Leftrightarrow (k-2)x=-2$

$\Leftrightarrow x=\frac{-2}{k-2}$ (đk: $k\neq 2$)

Khi đó: $y=-x+3=\frac{2}{k-2}+3$

Hai đths cắt nhau tại điểm có tung độ $7$

$\Leftrightarrow \frac{2}{k-2}+3=7$

$\Leftrightarrow \frac{2}{k-2}=4$

$\Leftrightarrow k-2=\frac{1}{2}\Leftrightarrow k=2,5$

a: Sửa đề: y=-x+3

Vẽ đồ thị

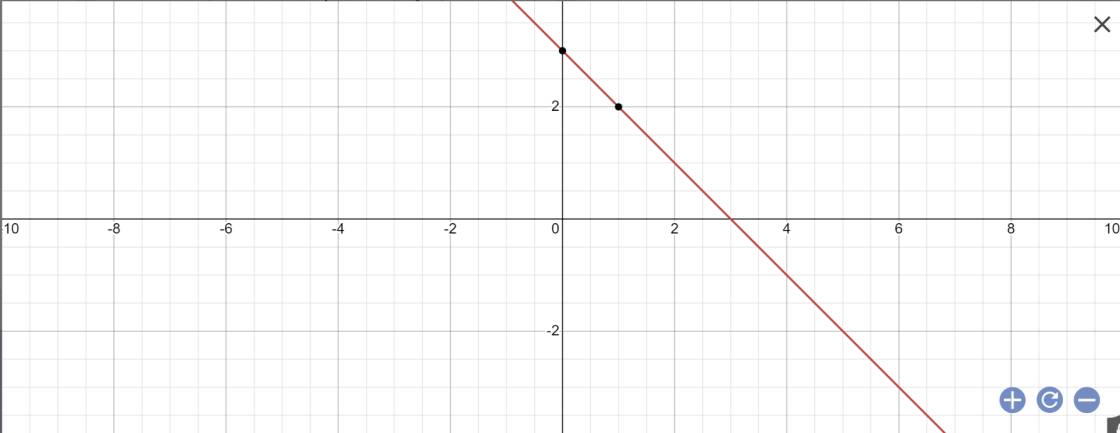
b: Để đường thẳng y=(2k-1)x+1 song song với (d) thì 

\(\left\{{}\begin{matrix}2k-1=-1\\1\ne3\left(đúng\right)\end{matrix}\right.\)

=>2k-1=-1

=>2k=0

=>k=0

c: Thay y=7 vào y=-x+3, ta được:

-x+3=7

=>-x=4

=>x=-2

Thay x=-2 và y=7 vào y=(k-3)x+5, ta được:

-2(k-3)+5=7

=>-2(k-3)=2

=>k-3=-1

=>k=2