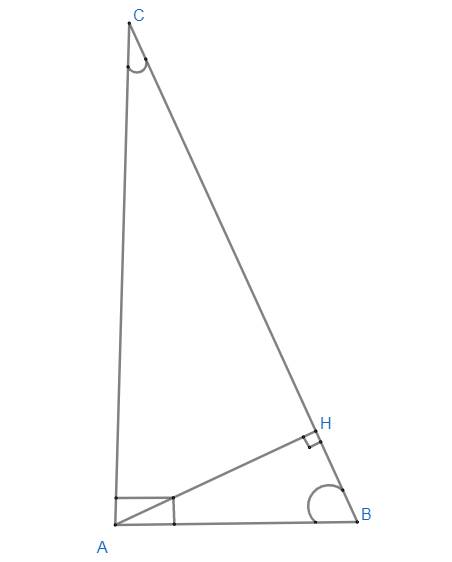
Cho ΔABC nhọn. Vẽ AH vuông góc BC, BI vuông góc AC. Chứng minh \(\widehat{IBC}=\widehat{HAC}\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
Cho tam giác nhọn ABC. Vẽ AHBC; BIAC. Chứng minh góc IBC bằng góc HAC
Xét tam giác AHC vuông tại H có \(\widehat{HAC}+\widehat{ACB}=90^0\)
Xét tam giác BIC vuông tại I có \(\widehat{IBC}+\widehat{ACB}=90^0\)
Do đó: \(\widehat{HAC}=\widehat{IBC}\)
Đúng 1
Bình luận (1)
Cho ΔABC vuông tại A (AB < AC)
Kẻ \(AH\perp BC\) tại H
a) Chứng minh \(\widehat{ABC}\) = \(\widehat{HAC}\)
b) Chứng minh \(\widehat{ACB}\) = \(\widehat{HAB}\)
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)
Đúng 2
Bình luận (2)
Cho tam giác ABC vuông tại A có AB<AC trên cạch BC lấy điểm D sao cho AB = BD,kẻ AH vuông góc với BC,kẻ DK vuông góc với AC.
a)Chứng minh:\(\widehat{BAD}=\widehat{BDA}\) b)C/M:AD là tia phân giác của \(\widehat{HAC}\)
c)C/M: AK=AH d)C/M:AB+AC<BC+AH
Giải thích các bước giải:
a, ΔBAD có BA = BD
⇒ ΔBAD cân ở B
⇒ (đpcm)
b, Ta có:
ΔAHD vuông ở H ⇒
ΔABC vuông ở A ⇒
mà
⇒
⇒ AD là tia phân giác của (đpcm)
c, Xét 2 tam giác vuông ΔHAD và ΔKAD có:
AH chung;
⇒ ΔHAD = ΔKAD (cạnh huyền - góc nhọn)
⇒ AH = AK (đpcm)
d, AB + AC = BD + AK + KC = BD + AH + KC < BD + AH + DC = BC + AH
Vậy AB + AC < BC + AH
Đúng 1
Bình luận (0)
Giải thích các bước giải:
a, ΔBAD có BA = BD
⇒ ΔBAD cân ở B
⇒ (đpcm)
b, Ta có:
ΔAHD vuông ở H ⇒
ΔABC vuông ở A ⇒
mà
⇒
⇒ AD là tia phân giác của (đpcm)
c, Xét 2 tam giác vuông ΔHAD và ΔKAD có:
AH chung;
⇒ ΔHAD = ΔKAD (cạnh huyền - góc nhọn)
⇒ AH = AK (đpcm)
d, AB + AC = BD + AK + KC = BD + AH + KC < BD + AH + DC = BC + AH
Vậy AB + AC < BC + AH
Đúng 0
Bình luận (0)
Giải thích các bước giải:
a, ΔBAD có BA = BD
⇒ ΔBAD cân ở B
⇒ (đpcm)
b, Ta có:
ΔAHD vuông ở H ⇒
ΔABC vuông ở A ⇒
mà
⇒
⇒ AD là tia phân giác của (đpcm)
c, Xét 2 tam giác vuông ΔHAD và ΔKAD có:
AH chung;
⇒ ΔHAD = ΔKAD (cạnh huyền - góc nhọn)
⇒ AH = AK (đpcm)
d, AB + AC = BD + AK + KC = BD + AH + KC < BD + AH + DC = BC + AH
Vậy AB + AC < BC + AH
chúc bn học tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác nhọn ABC có ABAC kẻ AH vuông góc với BC (HinBC) AE là tia phân giác góc HAC. Kẻ ED vuông góc với AC (DinAC). Chứng minh rằnga) Delta HAEDelta DAEb) ECHEc) So sánh widehat{BAH}và widehat{HAC}Viết giả thiết, kết luận vẽ hình GIÚP MÌNH VỚI
Đọc tiếp
Cho tam giác nhọn ABC có AB<AC kẻ AH vuông góc với BC (H\(\in\)BC) AE là tia phân giác góc HAC. Kẻ ED vuông góc với AC (D\(\in\)AC). Chứng minh rằng
a) \(\Delta HAE=\Delta DAE\)
b) EC>HE
c) So sánh \(\widehat{BAH}\)và \(\widehat{HAC}\)
Viết giả thiết, kết luận vẽ hình
GIÚP MÌNH VỚI
Cho tam giác ABC vuông tại A, đường cao AH, từ H kẻ đường thẳng vuông góc với AC tại K. Vẽ tia phân giác của \(\widehat{HAC}\)cắt HK tại I. từ I kẻ đường thẳng song song với BC cắt AC tại D. Chứng minh rằng: \(\widehat{AIH}=\widehat{AID}\)
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HE vuông góc với AB, HF vuông góc với AC (E thuộc AB, F thuộc AC).a) Chứng minh: widehat{AFE}widehat{ABC}b) Đường thẳng EF cắt BC tại M. Chứng minh: ME . MF MB . MC.c) Cho biết AC 10 cm, widehat{BAC60^o}, widehat{ABC}80^o . Tính độ dài đoạn vuông góc hạ từ A xuống EF.
Đọc tiếp
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HE vuông góc với AB, HF vuông góc với AC (E thuộc AB, F thuộc AC).
a) Chứng minh: \(\widehat{AFE}=\widehat{ABC}\)
b) Đường thẳng EF cắt BC tại M. Chứng minh: ME . MF = MB . MC.
c) Cho biết AC= 10 cm, \(\widehat{BAC=60^o}\), \(\widehat{ABC}=80^o\) . Tính độ dài đoạn vuông góc hạ từ A xuống EF.
b) Xét ΔMEB và ΔMCF có
\(\widehat{MEB}=\widehat{MCF}\left(=\widehat{AEF}\right)\)
\(\widehat{M}\) chung
Do đó: ΔMEB\(\sim\)ΔMCF(g-g)
Suy ra: \(\dfrac{ME}{MC}=\dfrac{MB}{MF}\)
hay \(ME\cdot MF=MB\cdot MC\)
Đúng 1
Bình luận (0)
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)(hai góc tương ứng)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Vẽ AH vuông góc BC tại H. Trên BC lấy điểm K sao cho BK=BA. Tên AC lấy điểm I sao cho AI=AK. Cm:
a) Tam giác ABC cân
b) \(\widehat{BAH}=\widehat{ACB}\)
c)Góc HAC=KAI
d) AC vuông góc với KI
e) BC-AC>AC-AH
f)AH+BC>AB+AC
theo minh la dap an A ;nho k minh nhe
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn.vẽ AH vuông góc BC, BI vuông góc AH.chứng minh IBC=HAC
GIÚP MK IK MÀ T_T
Nhưng AH đã vuông góc với BC rồi sao BI vuông góc với Ah nữa
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho ΔABC vuông tại A, AH ⊥ BC tại H. Trên cạnh BC lấy D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC ở E
a) So sánh AE và DE
b) Chứng minh tia AD là tia phân giác của góc HAC
c) Vẽ DK vuông góc với AC tại K. Chứng minh rằng AK = AH
a, vì BD=BA nên t.giác DBA caab tại B
=>\(\widehat{BDA}\)=\(\widehat{BAD}\)mà \(\widehat{EDB}\)=\(\widehat{A}\)=90 độ nên suy ra góc \(\widehat{EAD}\)=\(\widehat{EDA}\)
=>t.giác EAD cân tại E
=>AE=DE đpcm
b,vì ED và AH cùng vuông góc vs BC nên ED//AH
=> \(\widehat{EDA}\)=\(\widehat{DAH}\)(so le) mà \(\widehat{EDA}\)=\(\widehat{EAD}\)(t.giác AED cân tại E)
=>\(\widehat{DAH}\)=\(\widehat{EAD}\)
=> AD là p/g của góc HAC
c, xét 2 t.giác vuông AKD và AHD có:
AD chung
\(\widehat{KAD}\)=\(\widehat{HAD}\)(AD là p/g của \(\widehat{HAC}\))
=>t.giác AKD=t.giác AHD(CH-GN)
=>AK=AH
#HỌC TỐT#
Đúng 0
Bình luận (0)





















