\(A=3\left|1-2x\right|-5\)tìm giá trị LN hoăc NN
ai làm dc minh cho 2 lik e
\(A=3\left|1-2x\right|-5\)tìm giá trị LN hoăc NN
1.
a,Tìm giá trị nhỏ nhất của biểu thức \(C=\left(x+1\right)^2+\left(y-\frac{1}{3}\right)^2-10\)
b, Tìm giá trị lớn nhất của biểu thức \(D=\frac{5}{\left(2x-1\right)^2+3}\)
2. Cho biểu thức \(E=\frac{3-x}{x-1}\). Tìm các giá trị nguyên của x để
a, E có giá trị nguyên
b, E có giá trị nhỏ nhất
trình bày cách làm nữa nha . làm dc 1 câu cũng dc nha
1.
a,Tìm giá trị nhỏ nhất của biểu thức \(C=\left(x+1\right)^2+\left(y+\frac{1}{3}\right)^2-10\)
b, Tìm giá trị lớn nhất của biểu thức \(D=\frac{5}{\left(2x-1\right)^2+3}\)
2. Cho biểu thức \(E=\frac{3-x}{x-1}\) . Tìm các giá trị nguyên của x để
a, E có giá trị nguyên
b, E có giá trị nhỏ nhất
trình bày cách làm nữa nha . làm dc 1 câu cũng dc nha
giải các phương trình sau
a) \(\log_3\left(2x-5\right)=3\)
b) \(\log_4x^2=2\)
c) \(\log_7\left(3x-1\right)=\log_7\left(2x+5\right)\)
d) \(\ln\left(4x^2+2x-3\right)=\ln\left(3x^2-3\right)\)
e) \(\log\left(2x+3\right)=log\left(1-3x\right)\)
a: ĐKXĐ: \(x\notin\left\{\dfrac{5}{2}\right\}\)
\(\log_32x-5=3\)
=>\(log_3\left(2x-5\right)=log_327\)
=>2x-5=27
=>2x=32
=>x=16(nhận)
b: ĐKXĐ: x<>0
\(\log_4x^2=2\)
=>\(log_4x^2=log_416\)
=>\(x^2=16\)
=>\(\left[{}\begin{matrix}x=4\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{5}{2}\right\}\)
\(\log_7\left(3x-1\right)=\log_7\left(2x+5\right)\)
=>3x-1=2x+5
=>x=6(nhận)
d: ĐKXĐ: \(x\notin\left\{1;-1;\dfrac{-1+\sqrt{13}}{4};\dfrac{-1-\sqrt{13}}{4}\right\}\)
\(ln\left(4x^2+2x-3\right)=ln\left(3x^2-3\right)\)
=>\(4x^2+2x-3=3x^2-3\)
=>\(x^2+2x=0\)
=>x(x+2)=0
=>\(\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)
e: ĐKXĐ: \(x\notin\left\{-\dfrac{3}{2};\dfrac{1}{3}\right\}\)
\(log\left(2x+3\right)=log\left(1-3x\right)\)
=>2x+3=1-3x
=>5x=-2
=>\(x=-\dfrac{2}{5}\left(nhận\right)\)
TÌM GTLN HOĂC GTNN :
A = | 4x - 3 | + | 5y + 7,5 | + 10
B = \(\frac{5,8}{\left|2,5-x\right|+5,8}\)
C = 2 + \(\frac{12}{3\left|x+5\right|+4}\)
D = 6 - \(\frac{10}{5\left|6y-8\right|+1}\)
E = - 6 +\(\frac{24}{2\left|x-2y\right|+3\left|2x+1\right|}\)
GIẢI GIÚP MK NHÉ ! LÀM ĐC PHẦN NÀO THÌ LÀM !
\(A=\left|4x-3\right|+\left|5y+7,5\right|+10\)
Mà \(\left|4x-3\right|\ge0\)với mọi x
\(\left|5y+7,5\right|\ge0\)với mọi y
\(\Rightarrow A\)có GTNN là 10
Để A có GTNN thì :
\(4x-3=0\) \(5y+7,5=0\)
\(4x=3\) \(5y=-7,5\)
\(x=\frac{3}{4}\) \(y=-1,5\)
\(B=\frac{5,8}{\left|2,5-x\right|+5,8}\)
Mà \(\left|2,5-x\right|\ge0\)
\(\Rightarrow\)GTNN \(\left|2,5-x\right|+5,8=5,8\)
Để B có GTLN \(\Rightarrow2,5-x=0\)
\(\Rightarrow x=2,5\)
Tìm giá trị lớn nhất và nhỏ nhất của hàm số :
\(f\left(x\right)=\frac{\ln^2x}{x}\) trên đoạn \(\left[1;e^3\right]\)
Cho hàm số \(y = {x^2} + 2x - 3\).
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b) Vẽ các điểm \(A\left( { - 3;0} \right),B\left( { - 2; - 3} \right),C\left( { - 1; - 4} \right),\)\(D\left( {0; - 3} \right),E\left( {1;0} \right)\) của đồ thị hàm số \(y = {x^2} + 2x - 3\) trong mặt phẳng tọa độ Oxy.
c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số \(y = {x^2} + 2x - 3\) (Hình 11).
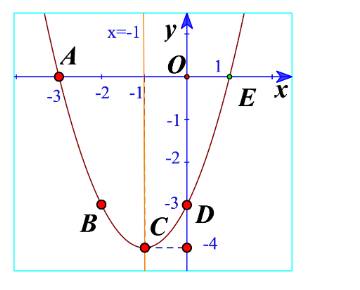
d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
a) Thay \(x = - 3\) vào hàm số ta được:
\(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Thay \(x = - 2\) vào hàm số ta được:
\(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = - 1\) vào hàm số ta được:
\(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng.
Thay \(x = 0\) vào hàm số ta được:
\(y = - 3\). Điền \( - 3\) vào ô tương ứng.
Thay \(x = 1\) vào hàm số ta được:
\(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng.
Vậy ta có:

b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.
Tính các nguyên hàm.
a)\(\int\dfrac{2dx}{x^2-5x}=A\ln\left|x\right|+B\ln\left|x-5\right|+C\) . Tìm 2A-3B.
b)\(\int\dfrac{x^3-1}{x+1}\)dx=\(Ax^3-Bx^2+x+E\ln\left|x+1\right|+C\).Tính A-B+E
a) \(\int\dfrac{2dx}{x^2-5x}=\int\left(\dfrac{-2}{5x}+\dfrac{2}{5\left(x-5\right)}\right)dx=-\dfrac{2}{5}ln\left|x\right|+\dfrac{2}{5}ln\left|x-5\right|+C\)
\(\Rightarrow A=-\dfrac{2}{5};B=\dfrac{2}{5}\Rightarrow2A-3B=-2\)
b) \(\int\dfrac{x^3-1}{x+1}dx=\int\dfrac{x^3+1-2}{x+1}dx=\int\left(x^2-x+1-\dfrac{2}{x+1}\right)dx=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2+x-2ln\left|x+1\right|+C\)
\(\Rightarrow A=\dfrac{1}{3};B=\dfrac{1}{2};E=-2\Rightarrow A-B+E=-\dfrac{13}{6}\)
1/ Cho x + y = 2
Chứng minh xy nhỏ hơn hoặc bằng 1.
2/
a) Tìm giá trị lớn nhất của \(A=3-\left(\frac{4}{9}x+\frac{2}{15}\right)^6.\)
b) Tìm giá trị lớn nhất của \(B=2,25-\frac{1}{4}\left(1+2x\right)^2.\)
c) tìm giá trị lớn nhất của \(C=\frac{1}{3+\frac{1}{2}\left(2x-3\right)^4}.\)
Mik đg cần gấp ai làm nhanh và đúng nhất mik sẽ tik cho 3 cái!
1/ Ta có: \(xy\le\frac{\left(x+y\right)^2}{4}=\frac{2^2}{4}=\frac{4}{4}=1\)
Dấu "=" xảy ra khi x=y=1
Máy mình bị lỗi nên ko nhìn được các bài tiếp theo
Chúc bạn học tốt :)
Ta có : x+y=2 => x=2-y. Thay vào bt ta đc : xy= (2-y).y = 2y -y^2
Vì y^2 >= 0 =>2y-y^2 nhỏ hơn hoặc bằng 0