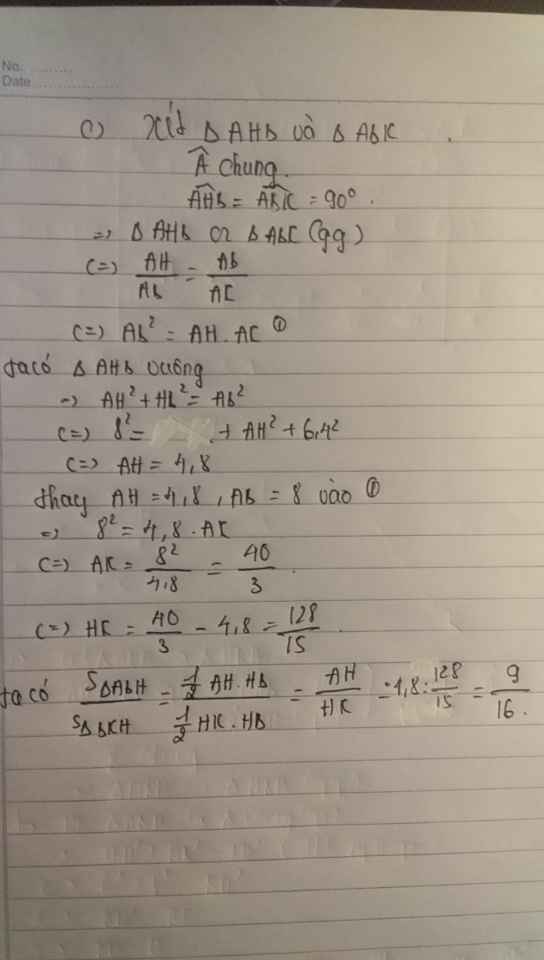Cho hình chữ nhật ABCD có AD = 12cm, AB = 16 cm. Kẻ đường cao AH cuuar tam giác ABD. Đường thắng AH cắt DC tại I và BC tại K. Chứng minh AH2 = HI.HK

Những câu hỏi liên quan
Cho hình chữ nhật ABCD có AB = 12cm, BC = 9cm. Gọi H là chân đường vuông góc kẻ từ A xuống BD a) C/m: tam giác AHB đồng dạng tam giác BCD b) Tính độ dài đoạn AH c) Tính diện tích tam giác AHB d) AH cắt đường thẳng BC tại K, cắt DC tại I. C/m: AH2 = HI.HK]
Cho hình chữ nhật ABCD có AB = 8cm, AD = 6cm. Kẻ đường cao AH của tam giác ABD.
a) Chứng minh rằng tam giác ABD đồng dạng với tam giác HBA.
b) Tính độ dài các đoạn thẳng BD, HB.
c) Đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. Tính tỉ số diện tích của hai tam giác ABH và BKH.
cho hình chữ nhật ABCD có AB=8cm AD=6cm. kẻ đường cao AH của tam giác ABD
a, chứng minh rằng tam giác ABD đồng dạng với tam giác HBA.
b, tính độ dài đoạn thẳng BD, HB.
c, đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. tính tỉ số diện tích của hai tam giác ABH và BKH
a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD có AB=8cm AD=6cm. kẻ đường cao AH của tam giác ABD
a, chứng minh rằng tam giác ABD đồng dạng với tam giác HBA.
b, tính độ dài đoạn thẳng BD, HB.
c, đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. tính tỉ số diện tích của hai tam giác ABH và BKH
a: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc HBA chung
Do đó: ΔABD\(\sim\)ΔHBA
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(HB=\dfrac{AB^2}{BD}=6.4\left(cm\right)\)
Đúng 0
Bình luận (0)
bài 1 : cho hình chữ nhật abcd có ab5cm bc12cm a). tính độ dài đoạn thẳng BD b). kẻ AH vuông BD tại H . Tính độ dài đoạn thẳng AH.c). đường thẳng AH cắt BC , DC lần lượt tại I và K . chứng minh rằng AH^2HI.HK
Đọc tiếp
bài 1 : cho hình chữ nhật abcd có ab=5cm bc=12cm
a). tính độ dài đoạn thẳng BD
b). kẻ AH vuông BD tại H . Tính độ dài đoạn thẳng AH.
c). đường thẳng AH cắt BC , DC lần lượt tại I và K . chứng minh rằng AH^2=HI.HK
a: ABCD là hình chữ nhật
=>\(BD^2=BA^2+BC^2\)
=>\(BD^2=5^2+12^2=169\)
=>BD=13(cm)
b: Xét ΔADB vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot13=5\cdot12=60\)
=>\(AH=\dfrac{60}{13}\left(cm\right)\)
c: \(\widehat{HDK}+\widehat{HBC}=90^0\)(ΔBDC vuông tại C)
\(\widehat{HIB}+\widehat{HBI}=90^0\)(ΔHBI vuông tại H)
mà \(\widehat{HBC}=\widehat{HBI}\left(I\in BC\right)\)
nên \(\widehat{HDK}=\widehat{HIB}\)
Xét ΔHDK vuông tại H và ΔHIB vuông tại H có
\(\widehat{HDK}=\widehat{HIB}\)
Do đó: ΔHDK đồng dạng với ΔHIB
=>\(\dfrac{HD}{HI}=\dfrac{HK}{HB}\)
=>\(HD\cdot HB=HK\cdot HI\)(1)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\left(2\right)\)
Từ (1) và (2) suy ra \(AH^2=HK\cdot HI\)
Đúng 1
Bình luận (0)
cho hình chữ nhật ABCD có AB=4cm AD=3cm. gọi H là chân đường vuông kẻ từ A đến cạnh BD.
a, chứng minh rằng tam giác ABD đồng dạng với tam giác HAD.
b, tính độ dài đoạn thẳng BD, HD.
c, đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. tính tỉ số diện tích của hai tam giác ABH và BKH
a) Xét ΔABD vàΔ HAD có:
\(\widehat{DAB}\) =\(\widehat{AHB}\)= 90o( gt)
\(\widehat{D}\) chung
⇒Δ ABD ∼ ΔHAD(g-g)
b) Áp dụng định lí Py-ta-go vào Δ ABD vuông tại A ta có:
BD=\(\sqrt{AD^2+AB^2}\)=\(\sqrt{3^2+4^2}\)=\(\sqrt{25}\)=5(cm)
Theo câu a ta có:Δ ABD ∼ ΔHAD
⇒\(\dfrac{BD}{AD}\)=\(\dfrac{AD}{HD}\)hay \(\dfrac{5}{3}\)=\(\dfrac{3}{HD}\)⇒HD=\(\dfrac{3.3}{5}\)=1,8 (cm)
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD có AB=4cm AD=3cm. gọi H là chân đường vuông kẻ từ A đến cạnh BD.
a, chứng minh rằng tam giác ABD đồng dạng với tam giác HAD.
b, tính độ dài đoạn thẳng BD, HD.
c, đường thẳng AH cắt DC tại I và cắt đường thẳng BC tại K. tính tỉ số diện tích của hai tam giác ABH và BKHv
a: Xét ΔABD vuông tại A và ΔHAD vuông tại H có
góc ADH chung
Do đó: ΔABD\(\sim\)ΔHAD
b: \(BD=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(HD=\dfrac{AD^2}{BD}=1.8\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB=12cm, BC=9cm. GỌi H là chân đường vuông góc kẻ từ S xuống Bd. Tia AH cắt DC tại F và cắt đường thẳng BC tại E. Chứng minh AH2 = EH . FH
a: Áp dụng định lí Pytago vào ΔBDC vuông tại C, ta được:
\(D B ^2 = B C ^2 + C D ^2\)
\(⇔ D B ^2 = 12 ^2 + 9 ^2 = 225\)
hay DB=15(cm)
Xét ΔBDC có
BE là đường phân giác ứng với cạnh DC
nên
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB 8cm, BC 15cma, Tính độ dài đoạn thẳng BDb, Vẽ AH vuông góc với BD tại H. Tính độ dài đoạn thẳng AHc, Đừng thẳng AH cắt BC và DC lần lượt tai I, K. Chứng minh:
A
H
2
H
I
.
H
K
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 8cm, BC = 15cm
a, Tính độ dài đoạn thẳng BD
b, Vẽ AH vuông góc với BD tại H. Tính độ dài đoạn thẳng AH
c, Đừng thẳng AH cắt BC và DC lần lượt tai I, K. Chứng minh: A H 2 = H I . H K
a, BD = 17cm
b, AH = 120 17 cm
c, HS tự làm
Đúng 0
Bình luận (2)