dùng hằng đẳng thức rút gọn biểu thức sau
9-\(x^2\)-6x
Những câu hỏi liên quan
18 tháng 11 2023 lúc 20:50
RÚT GỌN CÁC BIỂU THỨC SAU:
Gợi ý: Dùng hằng đẳng thức để rút gọn nhanh hơn (nhưng cũng phải biến đổi rõ ràng ra rồi mới ra hằng đẳng thức chứ ko đc làm nhanh bằng cách ghi hằng đẳng thức ngay!)
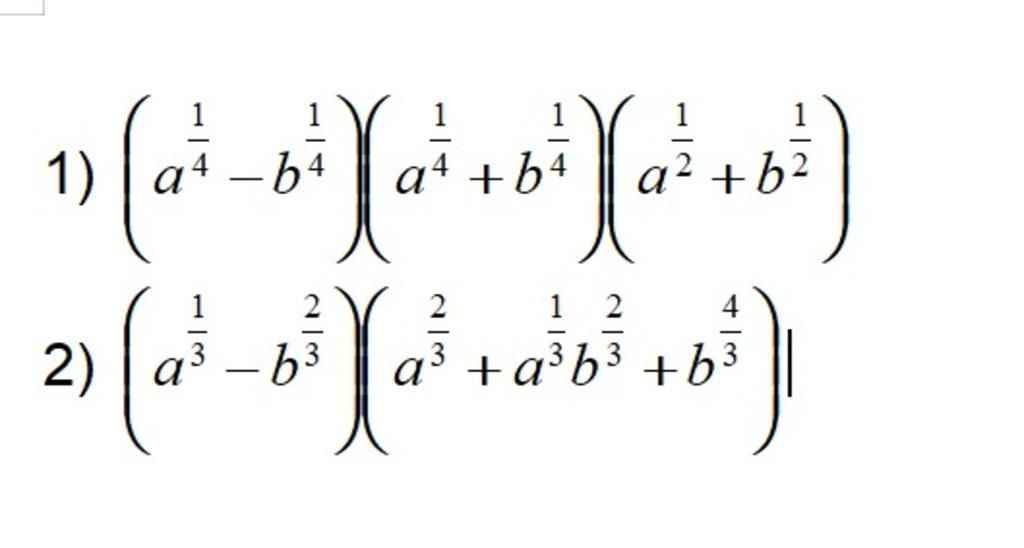
`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`
Đúng 4
Bình luận (0)
Rút gọn biểu thức sau 4x2 - ( x + 3 ) . ( x - 3 ) + x bằng phương pháp dùng hằng đẳng thức
\(4x^2-\left(x+3\right).\left(x-3\right)+x\)\(=4x^2-\left(x^2-3^2\right)+x\)
\(=4x^2-\left(x^2-9\right)+x\)
\(=4x^2-x^2+9+x\)
\(=3x^2+x+9\)
áp dụng hằng đẳng thức rồi rút gọn biểu thức sau:(4x-3)(3x+2)-(6x+1)(2x+5)+1
\(\left(4x-3\right)\left(3x+2\right)-\left(6x+1\right)\left(2x+5\right)+1\)
\(=\left(12x^2-9x+8x-6\right)-\left(12x^2+2x+30x+5\right)+1\)
\(=\left(-x-32x\right)+\left(-6-5+1\right)=-33x-10\)
rút gọn biểu thức sau, biết rằng biểu thức có chung một hằng đẳng thức
(3a-1)2+2(9a2-1)+(3a+1)2
\(=\left(3a-1\right)^2+2\left(3a-1\right)\left(3a+1\right)+\left(3a+1\right)^2\\ =\left(3a-1+3a+1\right)^2=\left(6a\right)^2=36a^2\)
Đúng 3
Bình luận (0)
Rút gọn biểu thức sau bằng cách áp dụng hằng đẳng thức đáng nhớ:
(x^2+1/x+1/9)(x-1/3)-(x-1/3)^3
Bài 3: Rút gọn biểu thức (Dùng hằng đẳng thức)1, (x+y)^2-(x-y)^22, (x+y)^3-(x-y)^3-2y^33,(x+y)^2-2(x+y)(x-y)+(x-y)^24,(2x+3)^2-2(2x+3)(2x+5)+(2x+5)^25, 9^8. 2^8-(18^4+1)(18^4-1)
Đọc tiếp
Bài 3: Rút gọn biểu thức (Dùng hằng đẳng thức)
1, (x+y)\(^2\)-(x-y)\(^2\)
2, (x+y)\(^3\)-(x-y)\(^3\)-2y\(^3\)
3,(x+y)\(^2\)-2(x+y)(x-y)+(x-y)\(^2\)
4,(2x+3)\(^2\)-2(2x+3)(2x+5)+(2x+5)\(^2\)
5, 9\(^8\). 2\(^8\)-(18\(^4\)+1)(18\(^4\)-1)
\(1,\left(x+y\right)^2-\left(x-y\right)^2=\left[\left(x+y\right)-\left(x-y\right)\right]\left[\left(x+y\right)+\left(x-y\right)\right]=\left(x+y-x+y\right)\left(x+y+x-y\right)=2y.2x=4xy\)
\(2,\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
\(3,\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\\ =\left[\left(x+y\right)-\left(x-y\right)\right]^2\\ =\left(x+y-x+y\right)^2\\ =4y^2\)
\(4,\left(2x+3\right)^2-2\left(2x+3\right)\left(2x+5\right)+\left(2x+5\right)^2\\ =\left[\left(2x+3\right)-\left(2x+5\right)\right]^2\\ =\left(2x+3-2x-5\right)^2\\ =\left(-2\right)^2\\ =4\)
\(5,9^8.2^8-\left(18^4+1\right)\left(18^4-1\right)\\ =18^8-\left[\left(18^4\right)^2-1\right]\\ =18^8-18^8+1\\ =1\)
Đúng 2
Bình luận (0)
1: =x^2+2xy+y^2-x^2+2xy-y^2=4xy
2: =x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3
=6x^2y
3: =(x+y-x+y)^2=(2y)^2=4y^2
4: =(2x+3-2x-5)^2=(-2)^2=4
5: =18^8-18^8+1=1
Đúng 0
Bình luận (0)
Dùng hằng đẳng thức rút gọn biểu thức:
( x2 + \(\frac{1}{x}\)+\(\frac{1}{9}\)) ( x - \(\frac{1}{3}\)) - ( x - \(\frac{1}{3}\))3
\(\left(x^2+\frac{1}{x}+\frac{1}{9}\right)\left(x-\frac{1}{3}\right)-\left(x-\frac{1}{3}\right)^3\)
\(=\left[x^3-\left(\frac{1}{3}\right)^3\right]-\left(x-\frac{1}{3}\right)^3\)
\(=\left(x-\frac{1}{3}\right)^3-\left(x-\frac{1}{3}\right)^3\)
Đúng 0
Bình luận (0)
\(=\left(x-\frac{1}{3}\right)\left[x^2+\frac{1}{x}+\frac{1}{9}-\left(x-\frac{1}{3}\right)^2\right]\)
\(=\left(x-\frac{1}{3}\right)\left(\frac{1}{x}+\frac{2x}{3}\right)\)
\(=\frac{3x-1}{3}\times\frac{3+2x^2}{3x}\)
\(=\frac{9x+6x^2-3-2x^2}{9x}\)
\(=\frac{4x^2+9x-3}{9x}\)
Đúng 0
Bình luận (0)
Bài 1: Rút gọn : a^2+ac-b^2-bc/a^2-b^2. Chứng minh hằng đẳng thức : x/x^2-2x - x^2+4/x^3-4x - 1/x^2-2x = 1/x^2+2x.
Bài 2: Cho biểu thức : K = 3/x-3 - 6x/9-x^2 + x/x+3. Tìm giá trị nguyên của x để K nhận giá trị dương
dùng hằng đẳng thức để khai triển và thu gọn biểu thức sau a, (6x2 +1/3)2 b,(5x-4y)2