giải tam giác vuông ABC,biết \(\widehat{A}\)=900 và:
a)a=15cm,b=10cm
Những câu hỏi liên quan
Giải tam giác vuông ABC, biết góc A = 90 độ và:
a, A= 15cm; B= 10cm
b, B= 12cm; C= 7cm
Cho tam giác ABC vuông tại A. Gọi BC a, AC b, AB c. Giải tam giác ABC, biết:a, b 10 cm,
C
^
30
0
b, a 20cm,
B
^
35
0
c, a 15cm, b 10cmd, b 12cm, c 7cm
Đọc tiếp
Cho tam giác ABC vuông tại A. Gọi BC = a, AC = b, AB = c. Giải tam giác ABC, biết:
a, b = 10 cm, C ^ = 30 0
b, a = 20cm,
B
^
=
35
0
c, a = 15cm, b = 10cm
d, b = 12cm, c = 7cm
a, Sử dụng tỉ số cosC và sinC, tính được
a = 20 3 3 cm, c = 10 3 3 cm và B ^ = 60 0
b, Sử dụng tỉ số sinB và cosB, tính được:
b = 20.sin 35 0 ≈ 11,47cm, c = 20.cos 35 0 ≈ 16,38cm
c, Sử dụng định lý Pytago và tỉ số sinB, tính được:
c = 5 5 cm, sinB = 10 15 => B ^ ≈ 41 , 8 0 , C ^ ≈ 48 , 2 0
d, Tương tự c) ta có
a = 193 cm, tanB = 12 7 => B ^ ≈ 59 , 7 0 , C ^ = 30 , 3 0
Đúng 0
Bình luận (0)
Ôn tập:1. Tìm x, y:2. Cho DeltaDMN vuông tại M, biết widehat{D} 37^o và DN 10cm. Giải tam giác vuông DMN?3. Cho DeltaABC perp tại B, AB 8cm, widehat{A} 53^o. Giải DeltaABC.
Đọc tiếp
Ôn tập:
1. Tìm x, y:
2. Cho \(\Delta\)DMN vuông tại M, biết \(\widehat{D}\)= 37\(^o\) và DN= 10cm. Giải tam giác vuông DMN?
3. Cho \(\Delta\)ABC \(\perp\) tại B, AB= 8cm, \(\widehat{A}\)= 53\(^o\). Giải \(\Delta\)ABC.
a) Áp dụng HTL ta có:\(MH.HP=MH^2\Rightarrow x=\sqrt{2.8}=4\)
\(BC=MH+HP=10\)
Áp dụng HTL ta có: \(HP.NP=MP^2\Rightarrow y=\sqrt{8.10}=4\sqrt{5}\)
b) Áp dụng HTL ta có: \(EQ.QF=DQ^2\Rightarrow x=\dfrac{4^2}{1}=16\)
\(EF=EQ+QF=17\)
Áp dụng HTL ta có: \(QP.EF=y^2\Rightarrow y=\sqrt{17.1}=\sqrt{17}\)
Đúng 2
Bình luận (0)
1) Giải tam giác vuông ABC, biết A= \(90^o\)và;
a) a= 15cm, b= 10cm
b) b= 12cm, c= 7cm
thanks
xin lỗi nhưng a=15 ,b=10 là sao zậy
Đúng 0
Bình luận (0)
Cô ra đề vậy, tui cũng k hiểu nên mới đăng lên hỏi
Đúng 0
Bình luận (0)
a là cạnh BC( vì BC đối diện vs góc A nên gọi là A)
tương tự b cx vậy
Đúng 0
Bình luận (0)
Tam giác vuông ABC ( ∠ A = 90 0 ) có AB = 6cm, AC = 8cm và tam giác vuông A’B’C’ ( ∠ A ' = 90 0 ) có A’B’ = 9cm, B’C’ = 15cm. Hỏi rằng hai tam giác vuông ABC và A’B’C’ có đồng dạng với nhau không? Vì sao?
* Trong tam giác vuông A’B’C’ có ∠ A ' = 90 0
Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2
Suy ra: A ' C ' 2 = B ' C ' 2 - A ' B ' 2 = 15 2 - 9 2 = 144
Suy ra: A’C’ = 12 (cm)
* Trong tam giác vuông ABC có ∠ A = 90 0
Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 =100
Suy ra: BC = 10 (cm)
Ta có: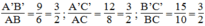 
Suy ra: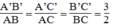 
Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)
Đúng 0
Bình luận (0)
Câu 4: a, Giải tam giác ABC vuông tại B. Biết góc A = 30°,AC= 10cm. b, Giải tam giác ABC vuông tại C. Biết góc B = 30°,AC =5cm
b: AB=10cm
\(BC=5\sqrt{3}\left(cm\right)\)
\(\widehat{C}=60^0\)
Đúng 0
Bình luận (0)
Giải tam giác ABC vuông tại A, biết rằng :
a) \(b=10cm,\widehat{C}=30^0\)
b) \(c=10cm,\widehat{C}=45^0\)
c) \(a=20cm,\widehat{B}=35^0\)
d) \(c=21cm,b=18cm\)
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm , BC = 10cm và tam giác DEF vuông tại D có DE = 9cm, DF = 12cm, EF = 15cm.
a) Hai tam giác ABC và DEF có đồng dạng không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác ấy?
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)
Đúng 0
Bình luận (0)
Giải tam giác vuông ABC, biết
A
^
90
0
và BC 50cm;
B
^
48
0
(làm tròn đến chữ số thập phân thứ nhất). A. AC 37,2cm; AB 33,4cm;
C
^
32
0
B. AC 37,2cm; AB 33,5cm;
C
^...
Đọc tiếp
Giải tam giác vuông ABC, biết A ^ = 90 0 và BC = 50cm; B ^ = 48 0 (làm tròn đến chữ số thập phân thứ nhất).
A. AC = 37,2cm; AB = 33,4cm; C ^ = 32 0
B. AC = 37,2cm; AB = 33,5cm; C ^ = 42 0
C. AB = 37,2cm; AC = 33,5cm; C ^ = 42 0
D. AC = 37,2cm; AB = 33,5cm; C ^ = 42 0
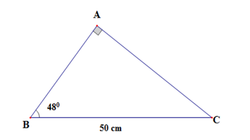
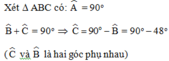
Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:
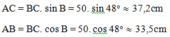
Vậy AC = 37,2cm; AB = 33,5cm; C ^ = 42 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)