Chứng minh rằng: Bán kính đường tròn ngoại tiếp tam giác đều có cạnh a bằng a√3/3

Những câu hỏi liên quan
Cho tam giác ABC có 3 góc đều nhọn. Gọi O là tâm đường tròn ngoại tiếp, H là trực tâm, P là trung điểm cạnh AC của tam giác ABC.
a. Chứng minh BH= 2OP
b. Gọi L là trung điểm của BH, chứng minh LP bằng bán kính đường tròn ngoại tiếp tam giác ABC
Giúp với !! Hứa sẽ tick
Cho tam giác đều ABC có cạnh bằng a. Hãy tính bán kính đường tròn ngoại tiếp tam giác đó.
Theo định lí sin ta có:
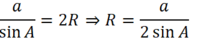
Tam giác ABC đều nên A = 60o ⇒ sin A = √3/2
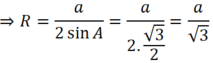
Đúng 0
Bình luận (0)
cho tam giác ABC có bán kính đường tròn ngoại tiếp bằng 1,thỏa sinA/mA+sinB/mB+sinC/mC=căn 3.chứng minh tam giác ABC đều
Cho hai tam giác ABC và DEF có các góc đều nhọn và có :
\(\widehat{ABC}=\widehat{DEF}\), \(\widehat{BAC}=\widehat{EDF}\) , \(AB=3DE\)
Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác ABC bằng 3 lần bán kính đường tròn ngoại tiếp tam giác DEF
Đề thi tuyển sinh vào 10 ptnk Hồ Chí Minh 2000-2001
https://text.123doc.org/document/1812116-de-thi-vao-chuyen-toan-10.htm
Bạn vào đây nhé :D
Cho tam giác đều ABC cạnh bằng 3cm. Bán kính của đường tròn ngoại tiếp tam giác ABC bằng:
A. 2 3 cm B. 2cm C. 3 cm D. 2 cm
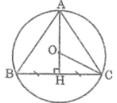
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
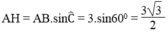
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
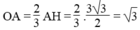
Vậy chọn đáp án C.
Đúng 0
Bình luận (0)
Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng. A.
a
3
3
B.
a
3
2
C.
a
3
4
D.
a
2
2
Đọc tiếp
Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.
A. a 3 3
B. a 3 2
C. a 3 4
D. a 2 2
Áp dụng định lí sin trong tam giác ta có a sin A = 2 R . Suy ra:
R = a 2 sin 60 ° = a 2. 3 2 = a 3 3 .
Chọn A.
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O, đường cao BH và CK lần lượt các đường tròn tại E và F
a) Chứng minh rằng tứ giác BKHC nội tiếp
b) Chứng minh OA vuông góc với EF và EF song song với HK
c) Gọi I là giao điểm của BH và CK. Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AIB bằng bán kính đường tròn ngoại tiếp tam giác BIC
Cho tam giác ABC cân đỉnh A, ^A=α, AB=m, D là một điểm trên cạnh BC sao cho BC=3BD
a) Tính BC, AD
b) Chứng tỏ rằng đường tròn ngoại tiếp các tam giác ABD, ACD là bằng nhau. Tính cosα để bán kính chúng bằng 1/2 bán kính R của đường tròn ngoại tiếp tam giác ABC
Cho tam giác đều ABC có cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC
Bán kính đường tròn ngoại tiếp của ΔABC là:
Đúng 0
Bình luận (0)
\(R=\dfrac{4\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng 4cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC















