Tính gtln-gtnn của HS
Giúp em với ạ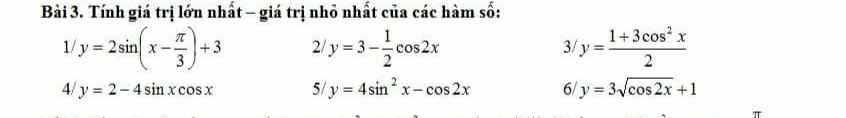

Những câu hỏi liên quan
Tính gtln-gtnn của hs lượng giác
Giúp em với em cảm ơn ạ
\(y=2-2.\left(2sinx.cosx\right)=2-2sin2x\)
Do \(-1\le sin2x\le1\Rightarrow0\le y\le4\)
\(y_{min}=0\) khi \(sin2x=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
\(y_{max}=4\) khi \(sin2x=-1\Rightarrow x=-\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
Tính gtln-gtnn của hs lượng giác
Giúp em với em cảm ơn ạ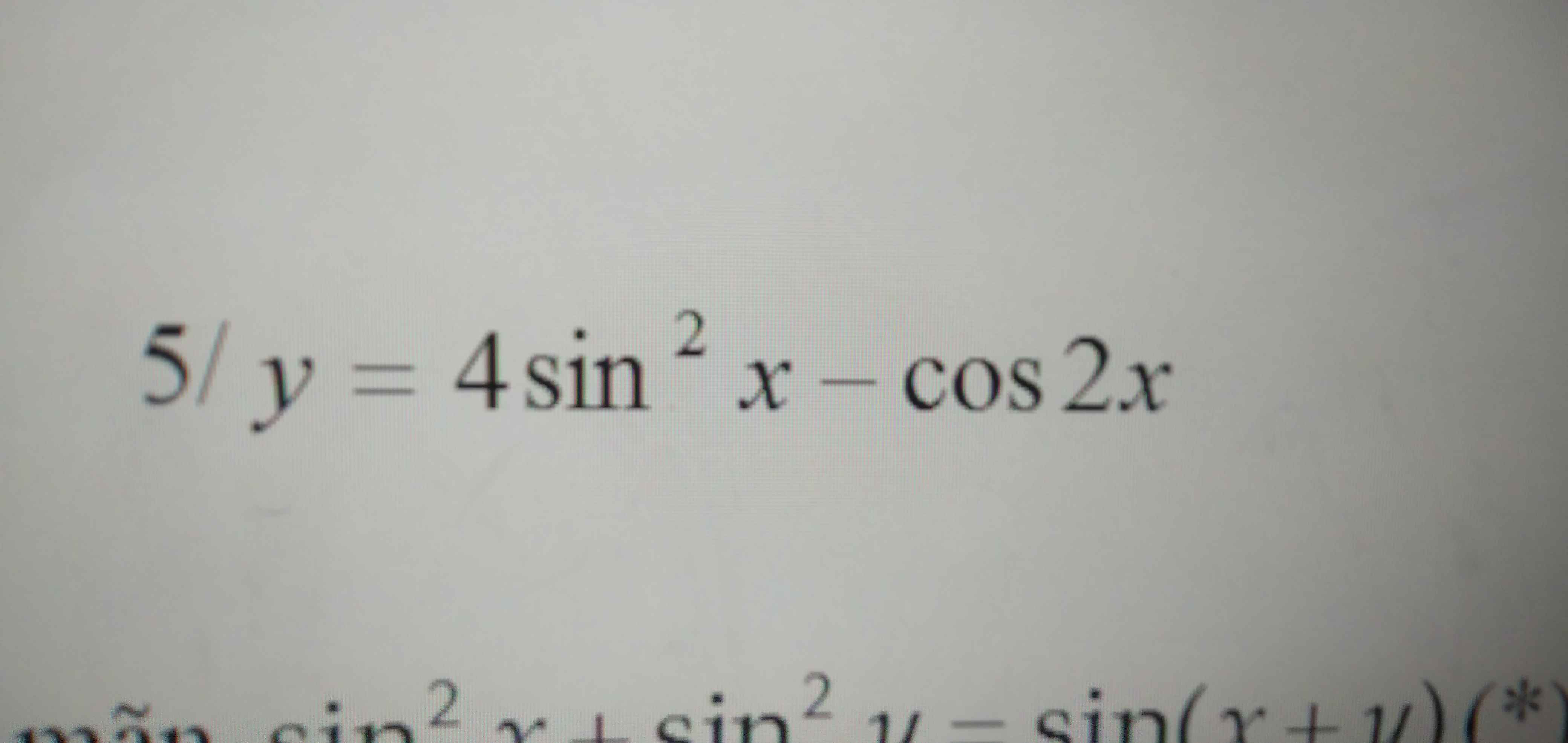
\(y=2\left(1-cos2x\right)-cos2x=2-3cos2x\)
Do \(-1\le cos2x\le1\Rightarrow-1\le y\le5\)
\(y_{min}=-1\) khi \(cos2x=1\Leftrightarrow x=k\pi\)
\(y_{max}=5\) khi \(cos2x=-1\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
Đúng 0
Bình luận (0)
Tính gtln-gtnn của hs lượng giác
Giúp em với em cảm ơn ạ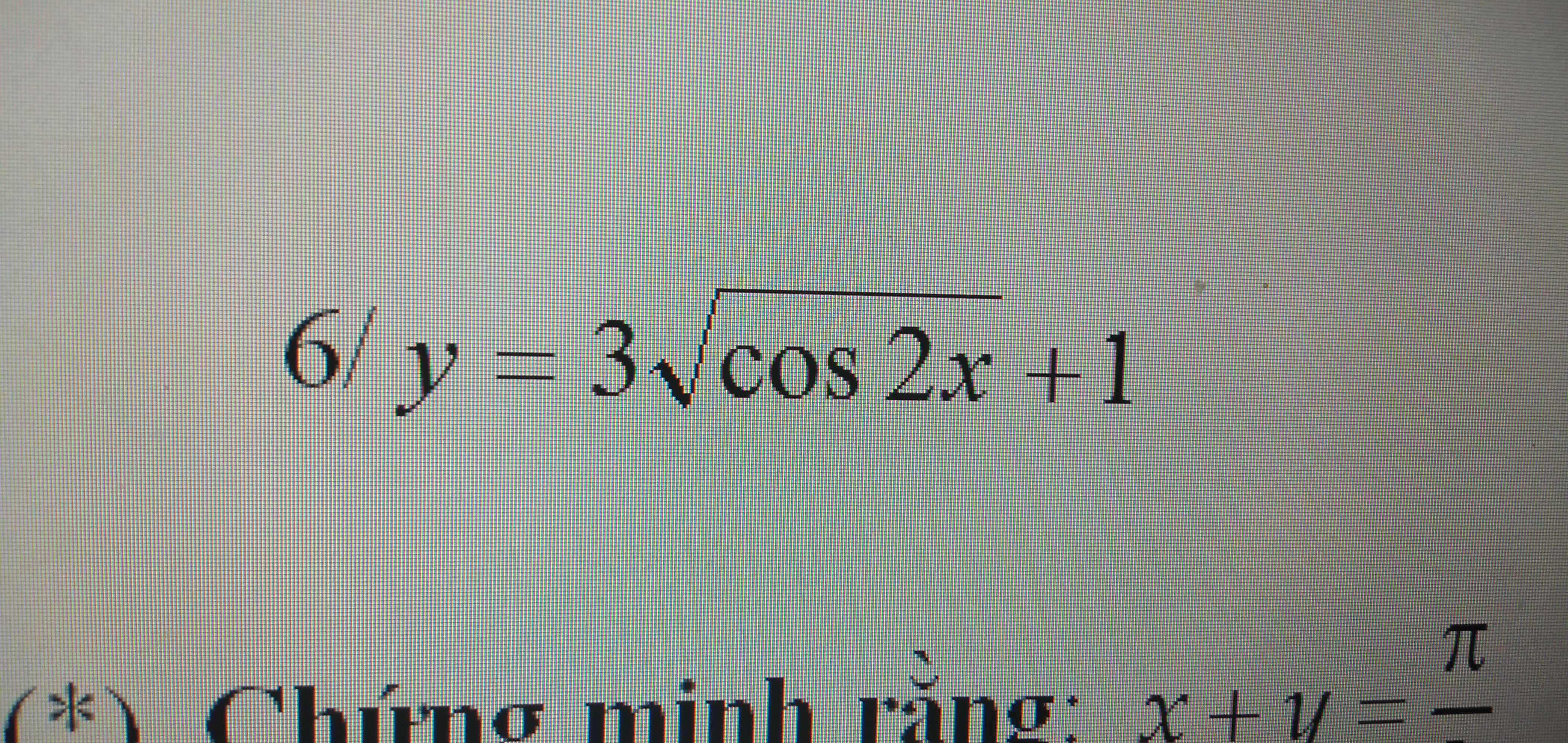
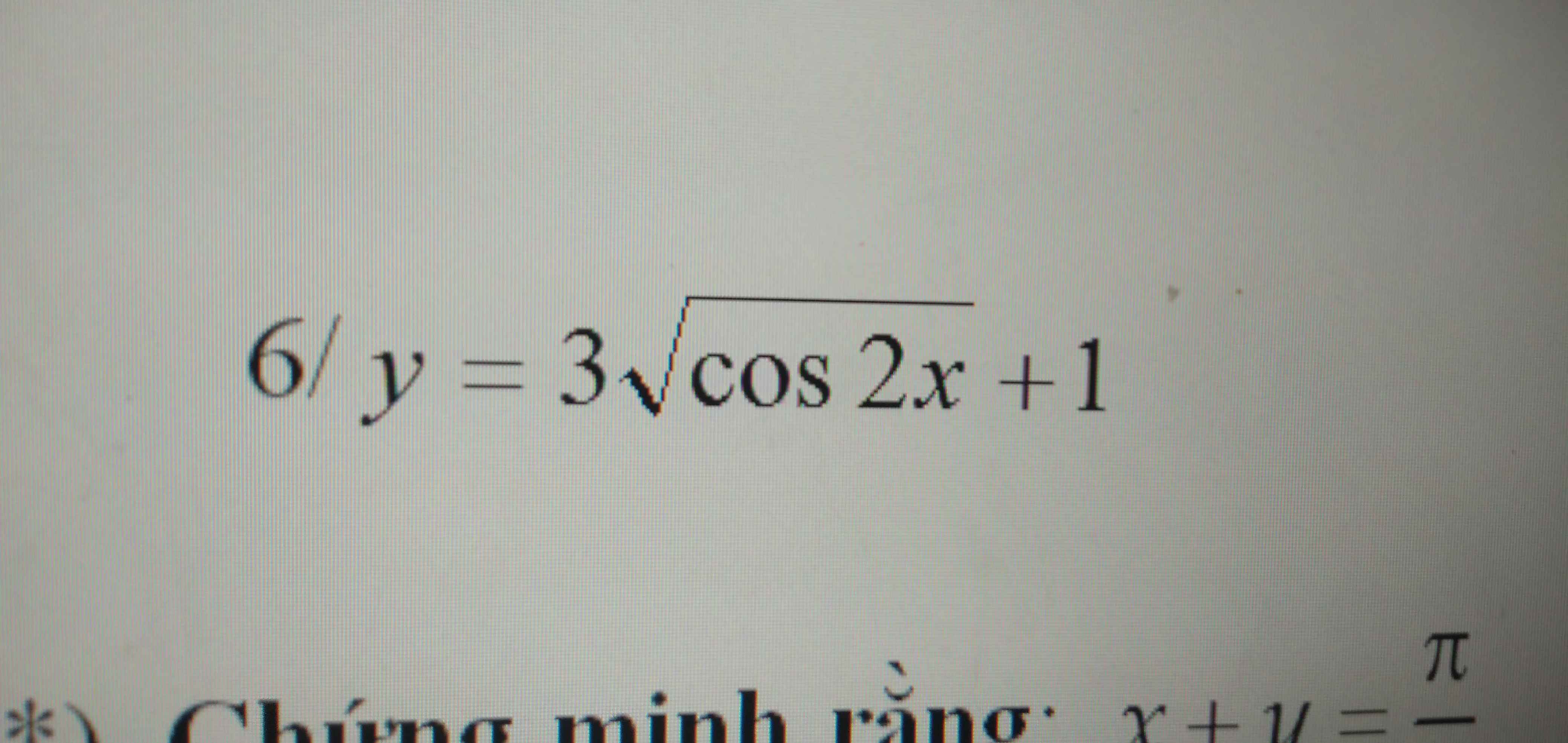
ĐKXĐ: \(cos2x\ge0\Rightarrow0\le cos2x\le1\)
\(\Rightarrow3.0+1\le y\le3.\sqrt{1}+1\)
\(\Rightarrow1\le y\le4\)
\(y_{min}=1\) khi \(cos2x=0\Rightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
\(y_{max}=4\) khi \(cos2x=1\Rightarrow x=k\pi\)
Đúng 0
Bình luận (0)
Gtln-gtnn của hs
Giúp em với ạ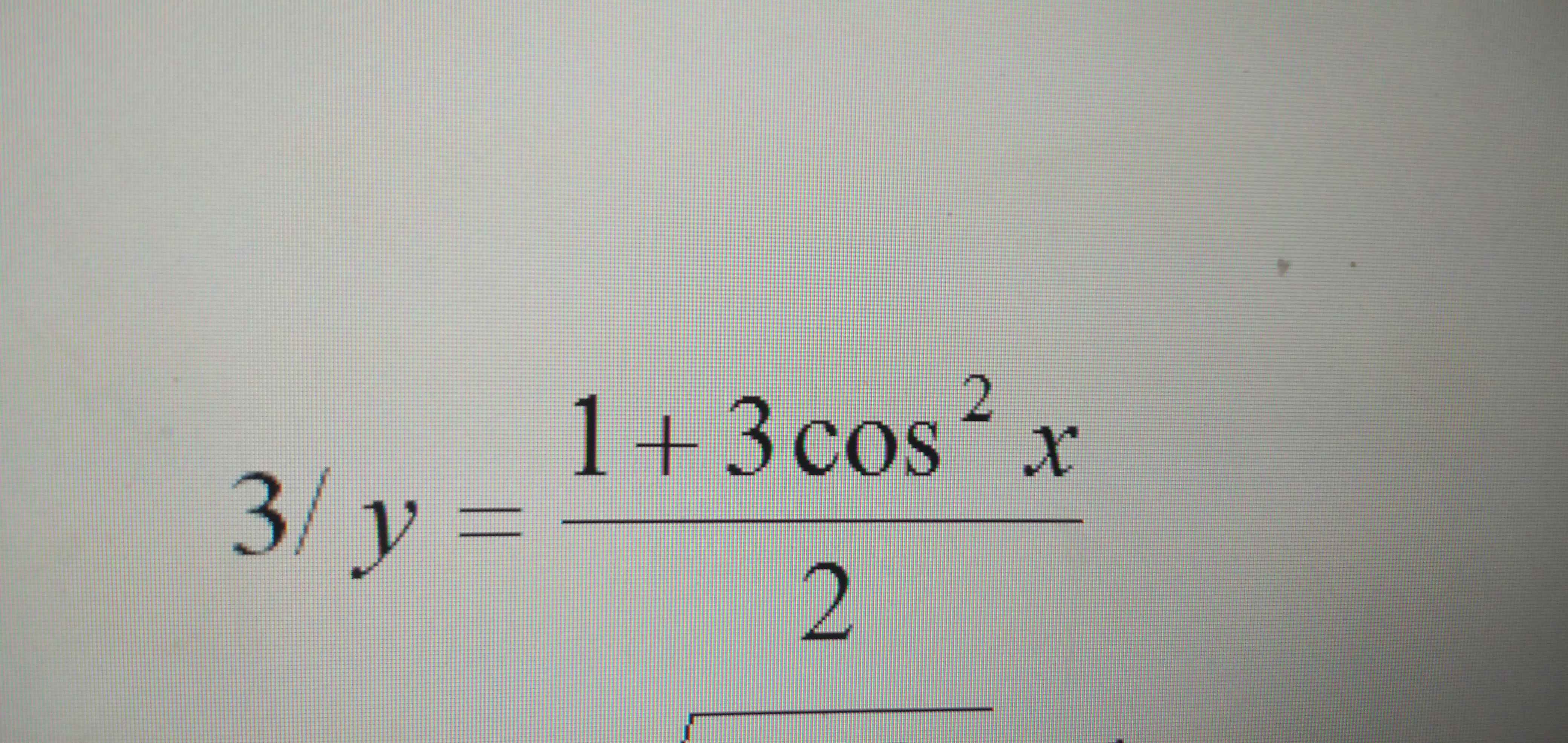
Do \(0\le cos^2x\le1\Rightarrow\dfrac{1}{2}\le y\le2\)
\(y_{min}=\dfrac{1}{2}\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
\(y_{max}=2\) khi \(cos^2x=1\Rightarrow sinx=0\Rightarrow x=k\pi\)
Đúng 0
Bình luận (0)
Có ai giúp em với ạ
em ko biết cách tính GTNN và GTLN lớp 8 .Mong các anh (chị ) giúp cho em với ạ
tình GTNN hay GTLN đều áp dụng hằng đẳng thức cơ bản và nâng cao, nếu học thoe lớp chuyên thì áp dụng cả những thứ trên trời dưới đất, trong ao ngoài hồ cũng có (vì mình học theo lớp đó) nhưng có thể phân biệt như sau
GTNN xảy ra khi có 1 số mũ chẵn + 1 số nào đó thì GTNN sẽ bằng số đó (VD tông quát là a2n+k(trong đó a có thể là 1 biểu thức, k là số bất kỳ)
GTLN xảy ra khi 1 số mũ lẻ + 1 số nào đó thì số mũ lẻ ấy phải = 0 để GTLN đạt được là cái số ko có biến đó (VD tổng quát a2n+1+k(trong đó a có thể là 1 biểu thức)
hơi khó hiểu nhỉ, ko hiểu chỗ nào cứ hỏi
Đúng 0
Bình luận (3)
Xem thêm câu trả lời
Giúp e tìm GTLN,GTNN sau đó tìm X các hs này giúp e vs ạ.Hơi dài nma e gấp quá ạ, e cảm ơn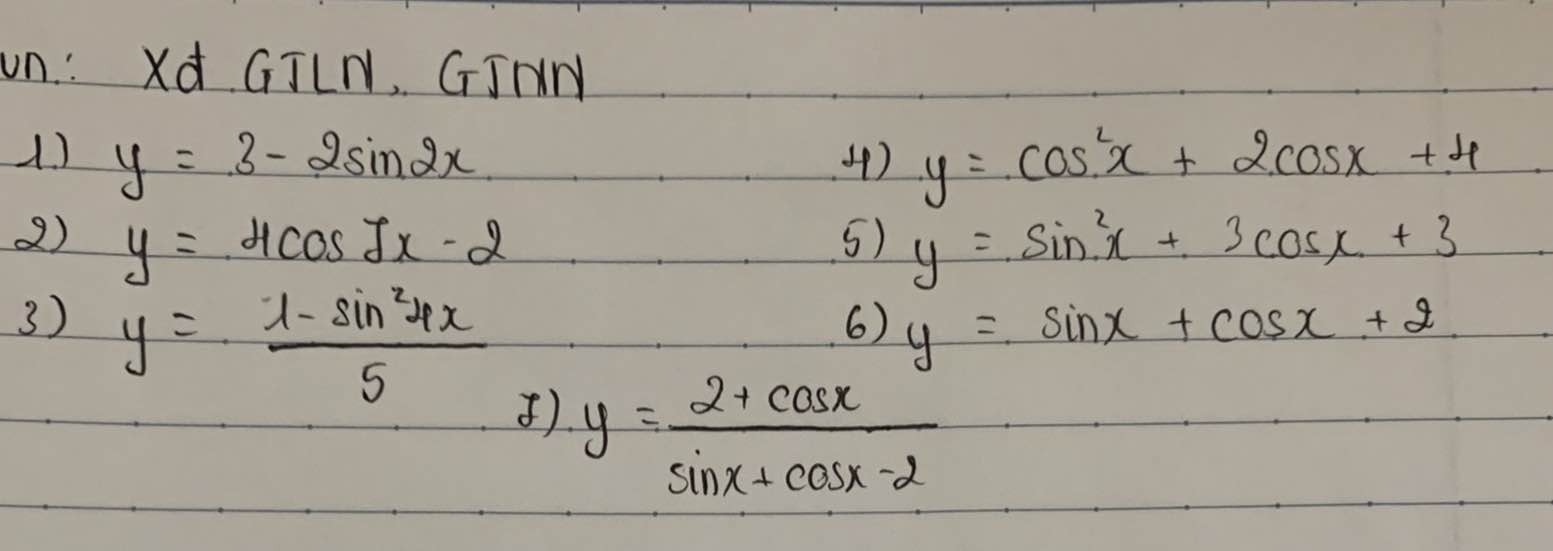
1)GTNN của hs y=x2+5/x-3 trên đoạn [3;6]
2)GTLN của hs y=sinx+căn3.cosx trên đoạn [0;bi]
3) Đk của m để pt x+căn1-x =m có nghiệm
Mn giúp mk vs ạ mk cảm ơn
tìm gtln (gtnn) của biểu thức: (x^4+1)^2+2021
mong mọi ng giúp em nhanh ạ
Lời giải:
$x^4\geq 0$ với mọi $x$
$\Rightarrow x^4+1\geq 1$
$\Rightarrow (x^4+1)^2\geq 1$
$\Rightarrow (x^4+1)^2+2021\geq 1+2021=2022$
Vậy GTNN của biểu thức là $2022$. Giá trị này đạt tại $x=0$
Đúng 0
Bình luận (0)
1. Tìm GTNN của biểu thức: A với 2. Tìm GTLN của biểu thức B với giúp mình với ạ, đg cần gấp ạ
Đọc tiếp
1. Tìm GTNN của biểu thức: A= với
2. Tìm GTLN của biểu thức B= với
giúp mình với ạ, đg cần gấp ạ
Câu này em đã hỏi rồi
Đúng 2
Bình luận (0)











