Cho pt \(x^4 -2(m^2+2)x^2 + m^4 +3=0 \)
Tìm giá trị m sao cho x12+x22+x32+x42+x1.x2.x3.x4=11
Những câu hỏi liên quan
Cho hàm số
y
x
4
-
2
(
2
m
+
1
)
x
2
+
4
m
2
(
1
)
. Các giá trị của tham số m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ
x
1
,
x
2
,
x
3
,
x
4
...
Đọc tiếp
Cho hàm số y = x 4 - 2 ( 2 m + 1 ) x 2 + 4 m 2 ( 1 ) . Các giá trị của tham số m để đồ thị hàm số (1) cắt trục hoành tại 4 điểm phân biệt có hoành độ x 1 , x 2 , x 3 , x 4 thỏa mãn là x 1 2 + x 2 2 + x 3 2 + x 4 2 = 6
A. m = 1 4
B. m > - 1 2
C. m > - 1 4
D. m ≥ - 1 4
Cho phương trình: x3- 5x2 + (2m+5)x-4m+2 = 0 (m là tham số )
a) Tìm đk của m để pt có 3 nghiệm phân biệt x1,x2,x3
b) Tìm gt của m để x12 + x22 + x32 = 11
\(x^3-5x^2+2mx+5x-4m+2=0\)
\(\Leftrightarrow\left(x^3-5x^2+5x+2\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x-1\right)+2m\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2-3x+2m-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-3x+2m-1=0\left(1\right)\end{matrix}\right.\)
a. Pt đã cho có 3 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb khác 2
\(\Leftrightarrow\left\{{}\begin{matrix}4-6+2m-1\ne0\\\Delta=9-4\left(2m-1\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m< \dfrac{13}{8}\end{matrix}\right.\)
b. Do vai trò 3 nghiệm như nhau, không mất tính tổng quát, giả sử \(x_1;x_2\) là nghiệm của (1) và \(x_3=2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2+x_3^2=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+4=11\)
\(\Leftrightarrow9-2\left(2m-1\right)-7=0\)
\(\Leftrightarrow m=1\)
Đúng 2
Bình luận (0)
Để đồ thị hàm số
(
C
)
:
y
x
3
-
2
x
2
+
(
1
-
m
)
x
+
m
(m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là
x
1
,
x
2
,
x
3...
Đọc tiếp
Để đồ thị hàm số ( C ) : y = x 3 - 2 x 2 + ( 1 - m ) x + m (m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 < 4 thì giá trị của m là:
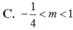
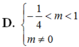
Cho hàm số y=(x-1)(x2+mx+m)
a. Với m=2, tính y', giải pt
b.Tìm m để tiếp tuyến tại điểm có hoành độ x=-1 song song với đường thẳng y=-2x-3
c. tìm m để pt y=0 có 3 nghiệm phân biệt x1,x2,x3 thỏa mãn x12 + x22 +x32 <4
d. tìm m để pt y=0 có 3 nghiệm phân biệt trong đó có 1 nghiệm lớn hơn 2
c3
cho PT ẩn x: x2-2(m-1)x-m-3=0 (1)
a/ giải phương trifnhd đã cho khi m =-3
b/ tìm giá trị của m để pt (1) có 2 nghiệm x1,x2 sao cho x12 + x22 =10
c/ tìm hệ thức liên hệ giữa các nghiệ ko phụ thuộc vfo giá trị của m
a: Khi m=-3 thì (1) trở thành \(x^2-2\cdot\left(-2\right)x-\left(-3\right)-3=0\)
=>x2+4x=0
=>x(x+4)=0
=>x=0 hoặc x=-4
b: \(\text{Δ}=\left(2m-2\right)^2-4\left(-m-3\right)\)
\(=4m^2-8m+4+4m+12\)
\(=4m^2-4m+16\)
\(=\left(2m-1\right)^2+15>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Ta có: \(x_1^2+x_2^2=10\)
nên \(\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(-m-3\right)=0\)
\(\Leftrightarrow4m^2-8m+4+2m+6=0\)
\(\Leftrightarrow4m^2-6m+10=0\)
\(\text{Δ}_1=\left(-6\right)^2-4\cdot4\cdot10=36-160< 0\)
Do đó: Phương trình vô nghiệm
Đúng 3
Bình luận (0)
Tìm giá trị của tham số m để đồ thị hàm số
y
x
3
-
3
m
x
2
+
m
2
-
1
x
+
m
2
-
m
cắt trục hoành tại ba điể...
Đọc tiếp
Tìm giá trị của tham số m để đồ thị hàm số y = x 3 - 3 m x 2 + m 2 - 1 x + m 2 - m cắt trục hoành tại ba điểm x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 = 10 .
Cho phương trình: x2+mx+1=0 (1), m là tham số
a)Giải phương trình (1) khi m=4.
b)Tìm giá trị m để pt (1) có 2 nghiệm x1,x2 thõa mãn: x12/x22 + x22/x12 >7
Xem chi tiết
Để đồ thị hàm số
(
C
)
:
y
x
3
-
2
x
2
+
(
1
-
m
)
x
+
m
(m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là
x
1
,
x
2
,
x
3...
Đọc tiếp
Để đồ thị hàm số ( C ) : y = x 3 - 2 x 2 + ( 1 - m ) x + m (m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 < 4 thì giá trị của m là:
A. m < 1
B. m > 1 m < - 1 4
C. - 1 4 < m < 1
D. - 1 4 < m < 1 m ≠ 0
cho PT: x2-2mx 2m-2=0(1) m là tham số
a) GPT(1) khi m=1
b)CM: PT(1) luôn có 2 nghiệm x1, x2 với các giá trị nào của tham số m thì x12 x22=12c) với x1, x2 là 2 nghiệm của pt (1) , tìm giá trị lớn nhất của biểu thức A= 6(x1 x2)/x12 x12 4(x1 x2)
Bài 1: Cho pt ẩn x: x2 - 2(m+1) x + m2 - m 0 (1)a) Giải pt (1) khi m -1, m 0b) Tìm m để pt (1) có 1 nghiệm là 1. Tìm nghiệm còn lại. c) Trong trường hợp pt (1) có 2 nghiệm hãy tính: x12 + x22; (x1-x2)2.Bài 2: Cho pt: x2 - 4x + 3 0Tính giá trị biểu thức:a) x12 + x22b) dfrac{1}{x1+2}+dfrac{1}{x2+2}c) x13 + x23.d) x1 - x2.
Đọc tiếp
Bài 1: Cho pt ẩn x: x2 - 2(m+1) x + m2 - m = 0 (1)
a) Giải pt (1) khi m = -1, m = 0
b) Tìm m để pt (1) có 1 nghiệm là 1. Tìm nghiệm còn lại.
c) Trong trường hợp pt (1) có 2 nghiệm hãy tính: x12 + x22; (x1-x2)2.
Bài 2: Cho pt: x2 - 4x + 3 = 0
Tính giá trị biểu thức:
a) x12 + x22
b) \(\dfrac{1}{x1+2}+\dfrac{1}{x2+2}\)
c) x13 + x23.
d) x1 - x2.
Bài 2:
a: \(x^2-4x+3=0\)
=>x=1 hoặc x=3
\(x_1^2+x_2^2=1^2+3^2=10\)
b: \(\dfrac{1}{x_1+2}+\dfrac{1}{x_2+2}=\dfrac{1}{1}+\dfrac{1}{5}=\dfrac{6}{5}\)
c: \(x_1^3+x_2^3=1^3+3^3=28\)
d: \(x_1-x_2=1-3=-2\)
Đúng 0
Bình luận (0)