Áp dụng bđt Cô-si \(1=x^2+y^2\ge2xy\)

              \(\Rightarrow xy\le\frac{1}{2}\)

Ta có \(A=\frac{-2xy}{1+xy}\ge\frac{-\frac{2.1}{2}}{1+\frac{1}{2}}=-\frac{2}{3}\)

\("="\Leftrightarrow x=y=\frac{1}{\sqrt{2}}\)

c) Theo hệ thức Vi- et ta có:

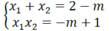
A =  x 1 2 + x 2 2 - 6 x 1 x 2  = x 1 + x 2 2 - 8 x 1 x 2  

= 2 - m 2  - 8(-m + 1) = m 2 - 4m + 4 + 8m - 8

=  m 2  + 4m - 4 = m + 2 2 - 8

Ta có: (m + 2)2 ≥ 0 ∀ m

⇒  m + 2 2 - 8 ≥ -8 ∀ m ⇔ A ≥ -8 ∀ m

Dấu bằng xảy ra khi  m + 2 2  = 0 ⇔ m= -2

Vậy GTNN của A là -8, đạt được khi m = -2

A>=1/(1+xy)=1/2

Dấu = xảy ra khi x=y=1

\(y\ge xy+1\ge2\sqrt{xy}\Rightarrow\sqrt{\dfrac{y}{x}}\ge2\Rightarrow\dfrac{y}{x}\ge4\)

\(Q=\dfrac{1-\dfrac{2y}{x}+2\left(\dfrac{y}{x}\right)^2}{\dfrac{y}{x}+\left(\dfrac{y}{x}\right)^2}\)

Đặt \(\dfrac{y}{x}=a\ge4\)

\(Q=\dfrac{2a^2-2a+1}{a^2+a}=\dfrac{2a^2-2a+1}{a^2+a}-\dfrac{5}{4}+\dfrac{5}{4}=\dfrac{\left(a-4\right)\left(3a-1\right)}{4\left(a^2+1\right)}+\dfrac{5}{4}\ge\dfrac{5}{4}\)

\(Q_{min}=\dfrac{5}{4}\) khi \(a=4\) hay \(\left(x;y\right)=\left(\dfrac{1}{2};2\right)\)

Đáp án: B

b) Theo định lí Vi-et ta có:

x 1  + x 2 = m + 1 và x 1 . x 2  = m - 2

Do đó A =  x 1 2 + x 2 2 - 6 x 1 x 2  = x 1 + x 2 2 - 8 x 1 x 2

= m + 1 2 - 8(m – 2) = m 2  + 2m + 1 – 8m + 16

= m 2 - 6m + 17 = m - 3 2  + 8 ≥ 8

Vậy giá trị nhỏ nhất của A bẳng 8 khi m – 3 = 0 hay m = 3.

bằng 1 nha bạn

\(1\ge x+\dfrac{1}{y}\ge2\sqrt{\dfrac{x}{y}}\Rightarrow\dfrac{x}{y}\le\dfrac{1}{4}\)

Đặt \(\dfrac{x}{y}=a\Rightarrow0< a\le\dfrac{1}{4}\)

\(P=\dfrac{\left(\dfrac{x}{y}\right)^2-\dfrac{2x}{y}+2}{\dfrac{x}{y}+1}=\dfrac{a^2-2a+2}{a+1}=\dfrac{4a^2-8a+8}{4\left(a+1\right)}=\dfrac{4a^2-13a+3+5\left(a+1\right)}{4\left(a+1\right)}\)

\(P=\dfrac{5}{4}+\dfrac{\left(1-4a\right)\left(3-a\right)}{4\left(a+1\right)}\ge\dfrac{5}{4}\)

Dấu "=" xảy ra khi \(a=\dfrac{1}{4}\) hay \(\left(x;y\right)=\left(\dfrac{1}{2};2\right)\)