3x2+14x-15
3x2+14x-15
a)5x3+40y;
b)16x2+8xy+y2-16;
c)3x2+14x-15
\(a,=5\left(x^3+8y\right)\\ b,=\left(4x+y\right)^2-16=\left(4x+y-4\right)\left(4x+y+4\right)\\ c,=3\left(x^2+2\cdot\dfrac{7}{3}x-5\right)\\ =3\left(x^2+2\cdot\dfrac{7}{3}x+\dfrac{49}{9}-\dfrac{94}{9}\right)\\ =3\left(x+\dfrac{7}{3}-\dfrac{\sqrt{94}}{3}\right)\left(x+\dfrac{7}{3}+\dfrac{\sqrt{94}}{3}\right)\)
a: \(5x^3+40y=5\left(x^3+8y\right)\)
b: \(16x^2+8xy+y^2-16\)
\(=\left(4x+y\right)^2-16\)
\(=\left(4x+y-4\right)\left(4x+y+4\right)\)
giải phương trình sau:
a)3x2-5x +2 =0
b)-3x2 +14x -8 =0
a) \(3x^2-5x+2=0\)
Vì \(a+b+c=3-5+2=0\)
\(\Rightarrow\) pt co 2 ngiệm pb : \(x_1=1\) ; \(x_2=\frac{2}{3}\)
Vậy \(S=\left\{1;\frac{2}{3}\right\}\)
b) \(-3x^2+14x-8=0\)
\(\Delta'=7^2-\left(-3\right)\times\left(-8\right)=49-24=25\)
\(\Rightarrow\) pt có 2 nghiệm pb : \(x_1=4\) ; \(x_2=\frac{2}{3}\)
Vậy \(S=\left\{4;\frac{2}{3}\right\}\)
Phân tích đa thức thành nhân tử : 3x2 – 14x – 5
\(3x^2-14x-5=3x\left(x-5\right)+\left(x-5\right)=\left(x-5\right)\left(3x+1\right)\)
\(3x^2-14x-5\)
\(=3x^2-15x+x-5\)
\(=3x\left(x-5\right)+x-5\)
\(=\left(x-5\right)\left(3x+1\right)\)
A= 3x^2 + 14x - 15
3A= (3x)^2 + 2.7.(3x) - 15.3
3A= (3x+7)^2 +(15.3-7.7)
3A= (3x+7 )^2 -2^2
3A= (3x+7-2 )((3x+7+2 )
A= ( 3x-5)( x+ 3)
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4 x
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Tính P(x) + Q(x) và P(x) – Q(x).
Ta đặt và thực hiện các phép tính P(x) + Q(x) và P(x) – Q(x).

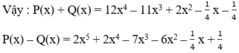
giải phương trình 3x2 11x √x−2 √2x 3 14x x≥2
b. 4x2 +4x+1=0 d. 5x2 6x1=0 a. 2x2-5x+1=0 c. -3x2 +2x+8=0 e. -3x2+ 14x - 8=0 g. -7x2 +4x-3=0
a. 2x2-5x+1=0
△= b2 - 4ac = (-5)2 - 4*2*1 = 17 ⇒√△ = √17
\(\Rightarrow x_1=\frac{5+\sqrt{17}}{4};x_2=\frac{5-\sqrt{17}}{4}\)
Vậy .... S={\(\frac{5\pm\sqrt{17}}{4}\)}
b. 4x2 +4x+1=0
⇔(2x+1)2 = 0 ⇔ x=\(\frac{-1}{2}\)
c. -3x2 +2x+8=0
△' = b'2 - ac = 12 - (-3)*8 = 25 ⇒√△ = 5
\(\Rightarrow x_1=\frac{-1+5}{-3}=-\frac{4}{3};x_2=\frac{-1-5}{-3}=2\)
Vậy... S={-\(\frac{4}{3}\);2}
d. 5x2 6x1=0 (thiếu dấu nên mk chưa giải được)
e. -3x2+ 14x - 8=0
△' = b'2 - ac = 72 - (-3)*(-8) = 25 ⇒ √△ = 5
⇒\(x_1=\frac{-7+5}{-3}=\frac{2}{3};x_2=\frac{-7-5}{-3}=4\)
Vậy .... S={\(\frac{2}{3};4\)}
g. -7x2 +4x-3=0
△' = b'2 - ac = 22 - (-7)*(-3) = -17<0
Vậy pt vô nghiệm , S=∅
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4 x
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x)
Giúp vs ạ
Bài 1 giải các bất phương trình sau
a.x2 - x - 6 = 0
b.2x2 - 7x + 5 < 0
c.3x2 - 9x + 6 ≥ 0
d.2x2 - 5x + 3 < 0
Bài 2 Giải phương trình sau
A.√x2 + x + 5 = √2x2 - 4x + 1
B.√11x2 -14x - 12 = √3x2 + 4x - 7
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4