Cho tam giác ABC AB< AC ,AD là tia phân giác góc A. . Trên tia AC lấy điểm E sao cho AE = AB
a,cmr BD= E
b, gọi K là giao điểm của các đường thẳng AB và EDF. Cmr tam giác DBK= tam giác DEC
Cho tam giác ABC có AB < AC và tia phân giác AD. TRên tia AC lấy E sao cho AE = AB
a) CMR: BD = DE
b) Gọi K là giao điểm của đường thẳng AB và ED. CMR: tam giác DBK = tam giác DEC.
c) Tam giác AKC là tam giác gì?
d) CMR: DE vuông góc KC
hình tự vẽ
a)Vì AD là tpg của ^BAC
=>^BAD = ^CAD = ^BAC/2
Xét tam giác ABD và tam giác AED có:
AD:cạnh chung
^BAD=^CAD(cmt)
AB=AE(gt)
=>tam giác ABD=tam giác AED (c.g.c)
=>BD=BE (cặp cạnh t.ư)
b)Vì tam giác ABD=tam giác AED(cmt)
=>^ABD=^AED (cặp góc t.ư)
Ta có:^ABD+^KBD=1800 (kề bù)
=>^KBD=1800-^ABD (1)
^AED+^CED=1800 (kề bù)
=>^CED=1800-^AED(2)
Từ (1);(2);có ^ABD=^AED(cmt)
=>^KBD=^CED
Xét tam giác DBK và tam giác DEC có:
BD=BE(cmt
^KBD=^CED(cmt)
^BDK=^EDC (2 góc đđ)
=>tam giác DBK=tam giác DEC (g.c.g)
Từ tam giác DBK=tam giác DEC(cmt)
=>BK=EC (cặp cạnh t.ư)
Ta có: AB+BK=AK (B thuộc AK)
AE+EC=AC (E thuộc AC0
mà BK=EC(cmt);AB=AE(gt)
=>AK=AC
Xét tam giác AKC có:AK=AC(cmt)
=>tam giác AKC cân (ở A) (DHNB)
d)sai đề
Cho tam giác ABC có AB < AC và tia phân giác AD. TRên tia AC lấy E sao cho AE = AB
a) CMR: BD = DE
b) Gọi K là giao điểm của đường thẳng AB và ED. CMR: tam giác DBK = tam giác DEC.
c) Tam giác AKC là tam giác gì?
d) CMR: DE vuông góc KC
Bạn ơi? sao bạn lười suy nghĩ vậy? câu nào làm được thì đừng đăng
Khongbiet
999 - 888 - 111 + 111 - 111 + 111 - 111
= 111 - 111 + 111 -111 + 111 - 111
= 0 + 111 - 111 + 111 - 111
= 111 - 111 + 111 - 111
= 0 + 111 - 111
= 111 - 111
= 0
Đáp số: 0
cho tam giác ABC ,AB<AC, AD là tia phân giác của góc A . trên tia AC lấy điểm E sao cho AE=AB
a, chúng minh BD=DE
b, gọi K là giao điểm của các đường thẳng AB Và ED . chứng minh tam giác DBK = tam giác DEC
c,tam giác AKC là tam giác gì ? chứng minh:
d,chứng minh AD vuông góc với KC
Cho tam giác ABC có AB < AC và tia phân giác AD. TRên tia AC lấy E sao cho AE = AB
a) CMR: BD = DE
b) Gọi K là giao điểm của đường thẳng AB và ED. CMR: tam giác DBK = tam giác DEC.
c) Tam giác AKC là tam giác gì?
d) CMR: AD vuông góc KC.
hình tự vẽ
a)Vì AD là tpg của ^BAC
=>^BAD = ^CAD = ^BAC/2
Xét tam giác ABD và tam giác AED có:
AD:cạnh chung
^BAD=^CAD(cmt)
AB=AE(gt)
=>tam giác ABD=tam giác AED (c.g.c)
=>BD=BE (cặp cạnh t.ư)
b)Vì tam giác ABD=tam giác AED(cmt)
=>^ABD=^AED (cặp góc t.ư)
Ta có:^ABD+^KBD=1800 (kề bù)
=>^KBD=1800-^ABD (1)
^AED+^CED=1800 (kề bù)
=>^CED=1800-^AED(2)
Từ (1);(2);có ^ABD=^AED(cmt)
=>^KBD=^CED
Xét tam giác DBK và tam giác DEC có:
BD=BE(cmt
^KBD=^CED(cmt)
^BDK=^EDC (2 góc đđ)
=>tam giác DBK=tam giác DEC (g.c.g)
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: BD=ED
b: Xét ΔDBK và ΔDEC có
\(\widehat{DBK}=\widehat{DEC}\)
BD=ED
\(\widehat{BDK}=\widehat{EDC}\)
Do đó: ΔDBK=ΔDEC
c: Ta có: ΔDBK=ΔDEC
nên BK=EC
Ta có: AB+BK=AK
AE+EC=AC
mà AB=AE
và BK=EC
nên AK=AC
hay ΔAKC cân tại A
1) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAD}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)
2) Ta có: ΔABD=ΔAED(cmt)
nên \(\widehat{ABD}=\widehat{AED}\)(hai góc tương ứng)
Ta có: \(\widehat{ABD}+\widehat{KBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)(cmt)
nên \(\widehat{KBD}=\widehat{CED}\)
Xét ΔDBK và ΔDEC có
\(\widehat{KBD}=\widehat{CED}\)(cmt)
BD=ED(cmt)
\(\widehat{BDK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDBK=ΔDEC(g-c-g)
3) Ta có: ΔDBK=ΔDEC(cmt)
nên BK=EC(hai cạnh tương ứng)
Ta có: AB+BK=AK(B nằm giữa A và K)
AE+EC=AC(E nằm giữa A và C)
mà AB=AE(gt)
và BK=EC(cmt)
nên AK=AC
Xét ΔAKC có AK=AC(cmt)
nên ΔAKC cân tại A(Định nghĩa tam giác cân)
Cho tam giác ABC có AB <AC . Phân giác AD . Trên tia AC lấy điểm E sao cho AE =AB
A, cm : BD=DE
B, gọi K là giao điểm của các đường thẳng AB và ED. Cm tam giác DBK= tam giác DEC
C, tam giác ÁC là tam giác gì?
D, cm DE vuông góc với KC
cho tam giác ABC có AB < AC . Phân giác AD . Trên tia AC lấy điểm E sao cho AE = AB
a) Chứng minh : BD = DE
b) Gọi K là giao điểm của các đường thẳng AB và ED . Chứng minh tam giác DBK = tam giác DEC
c) tam giác AKC là tam giác gì
d) Chứng minh : AD vuông góc KC
cho mk hoi:cho h=6a-13/5a-17 tim gia tri lon nhat cua h
Cho tam giác ABC , AB < AC, AD là tia phân giác của góc A. Trên tia AC lấy điểm E sao cho AE=AB
a) Chứng minh BD=DE
b) Gọi K là giao điểm của các đường thẳng AB và ED. Chứng minh △DBK=△DEC
cứu tui vớiii
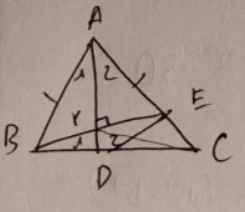
a Xét tam giác ABD và tam giác AED có:
\(\widehat{A_1}=\widehat{A_2}\)
AB = AE
BD chung
=> ΔABD = ΔAED (c.g.c)
=> BD = DE
b Xét △DBK và △DEC có:
DB = DE (cmt)
KD chung
\(\widehat{D_1}=\widehat{D_2}\)
=> △DBK=△DEC (c.g.c)
Cho tam giác ABC (AB<AC). Có AD là phân giác của góc A (D thuộc BC) Trên tia AC lấy điểm E sao cho AE = AB
a) CM: BD=DE
b) Gọi K là giao điểm của các đường thẳng AB và ED. CM: Tam giác ABC= Tam giác AEK và tam giác DBK= tam giác DEC.
c) Tam giác AKC là tam giác gì? CM điều đó
d) Chứng minh AD vuông góc với KC
b/ Xét 2 TG ABC và TG AEK,ta có:
A chung
E=B (2 TG = nhau câu a)
AB=AE (gt)
=>TG ABC=TG AEK (g-c-g)
=>AK=AC (cặp cạnh tương ứng)
Ta có :AK=AB+AC
AC=AE+EC
Mà AC=Ak
AB=AE
=>BK=EC
Xét 2 TG DBK và TG DEC,ta có:
BK=EC(cmt)
Góc BDK = góc EDC (đối đỉnh)
BD=ED(câu a)
=>TG DBK=TG DEC (c-g-c)
c/Vì AK=AC (TG AKE=TG ACB) nên TG AKC cân tại A
Cho tam giac ABC có AB < AC; AD là phân giác của goc A. Trên cạnh AC lấy điểm E sao cho AB = AE.
a. Chứng minh tam giac ABD = tam giac AED
b. Trên tia AB lấy điểm F sao cho AF = AC. Chứng minh tam giac FBD = tam giac CED và DF = DC
c. Chứng minh AD vuong goc voi CE d. Chứng minh BE // CF.
( giup minh voi cac ban oi )
b/ Xét 2 TG ABC và TG AEK,ta có:
A chung
E=B (2 TG = nhau câu a)
AB=AE (gt)
=>TG ABC=TG AEK (g-c-g)
=>AK=AC (cặp cạnh tương ứng)
Ta có :AK=AB+AC
AC=AE+EC
Mà AC=Ak
AB=AE
=>BK=EC
Xét 2 TG DBK và TG DEC,ta có:
BK=EC(cmt)
Góc BDK = góc EDC (đối đỉnh)
BD=ED(câu a)
=>TG DBK=TG DEC (c-g-c)
c/Vì AK=AC (TG AKE=TG ACB) nên TG AKC cân tại A
Câu 1: Vẽ phân giác AD của tam giác ABC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE=AB.
a, Chứng minh: BD = DE
b, Gọi K là giao điểm của các đường thẳng AB và ED. Chứng minh: tam giác DBK = tam giác DEC và tam giác ADC = tam giác ADK
c, Chứng minh AD là đường trung trực của BE
giúp tui với mọi người ơi
Lười đánh máy thật sự:vvv
a) Xét ∆ABD và ∆AED:
AD: cạnh chung
AB=AE(gt)
\(\widehat{BAD}=\widehat{CAD}\) (AD là phân giác góc BAC)
=> ∆ABD=∆AED (c.g.c)
=> BD=DC
b) Theo câu a: ∆ABD=∆AED
=> \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\left\{{}\begin{matrix}\widehat{ABD}+\widehat{DBK}=180^o\\\widehat{AED}+\widehat{DEC}=180^o\end{matrix}\right.\)
\(\Rightarrow\widehat{DBK}=\widehat{DEC}\)
Xét ∆DBK và ∆DEC:
BD=ED(cm ở a)
\(\widehat{DBK}=\widehat{DEC}\left(cmt\right)\)
\(\widehat{BDK}=\widehat{EDC}\) ( 2 góc đối đỉnh)
=> ∆DBK=∆DEC (g.c.g)
c) Gọi giao điểm của AD và BE là I
Xét ∆BAI và ∆EAI:
AB=AE(gt)
\(\widehat{BAI}=\widehat{EAI}\left(gt\right)\)
AI: cạnh chung
=> ∆BAI=∆EAI (c.g.c)
=> \(\left\{{}\begin{matrix}BI=EI\left(1\right)\\\widehat{AIB}=\widehat{AIE}\end{matrix}\right.\)
Mà \(\widehat{AIB}+\widehat{AIE}=180^o\) (2 góc kề bù)
=> \(\widehat{AIB}=\widehat{AIE}=90^o\left(2\right)\)
Từ (1) và (2) suy ra AD là trung trực của BE.
a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AE chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)