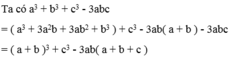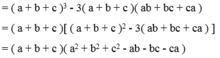Phân tích đa thức thành nhân tử: 2.(a2c + b2a + c2b ) - ( a2b + b2c +c2a)- 3abc

Những câu hỏi liên quan
phân tích đa thức thành nhân tử: a2b+a2c+ab2+ac2+c2b+cb2+2abc
Bài 1: (2 điểm) Phân tích các đa thức sau thành nhân tử
a) a3 – a2c + a2b – abc C,x2 + 1)2 – 4x2
b) x2 – 10x – 9y2 + 25 D, 4x2 – 36x + 56
giúp mik vs ạ ^^
\(a,a^2\left(a-b\right)+ab\left(a-c\right)=a\left(a+b\right)\left(a-c\right)\\ c,=\left(x^2-2x+1\right)\left(x^2+2x+1\right)=\left(x-1\right)^2\left(x+1\right)^2\\ b,=\left(x-5\right)^2-9y^2=\left(x-5-3y\right)\left(x-5+3y\right)\\ d,=4\left(x^2-9x+14\right)=4\left(x-7\right)\left(x-2\right)\)
Đúng 3
Bình luận (0)
Phân tích đa thức
a
4
+
a
3
+
a
3
b
+
a
2
b
thành nhân tử bằng phương pháp nhóm hạng tử A.
a
2
a
+
b
a
+
1...
Đọc tiếp
Phân tích đa thức a 4 + a 3 + a 3 b + a 2 b thành nhân tử bằng phương pháp nhóm hạng tử
A. a 2 a + b a + 1
B. a a + b a + 1
C. a 2 + a b a + 1
D. a + b a + 1
Ta có
a 4 + a 3 + a 3 b + a 2 b = a 4 + a 3 + a 3 b + a 2 b = a 3 a + 1 + a 2 b a + 1 = a + 1 a 3 + a 2 b = a + 1 a 2 a + b = a 2 a + b a + 1
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 45a3-30a2+5a-500
b) a2b-49b+14b2-b3
a) \(45a^3-30a^2+5a-500=5\left(9a^3-6a^2+a-100\right)\)
b) \(a^2b-49b+14b^2-b^3=b\left(a^2-b^2+14b-49\right)=b\left[a^2-\left(b-7\right)^2\right]=b\left(a-b+7\right)\left(a+b-7\right)\)
Tick hộ tui nha 😘
Đúng 3
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 7a3-28a2+28a
b) 45a3-30a2+5a-500
c) a2b-49b+14b2-b3
d) x4+4
a) $7a^3 - 28a^2 + 28a$
$ = 7a.(a^2 - 4a+4)$
$ = 7a.(a-2)^2$
d) $x^4 + 4$
$ = (x^4+4x^2+4) - 4x^2$
$ = (x^2+2)^2 - (2x)^2$
$ = (x^2+2x+2)(x^2-2x+2)$
Đúng 1
Bình luận (0)
Cho a, b, c, d là các số thực thỏa mãn 0 ≤ a, b, c ≤ 1. Tìm giá trị lớn nhất của biểu thức T = 2( a3 + b3 + c3 ) – ( a2b + b2c + c2a ).
Do \(0\le a,b,c\le1\)
nên\(\left\{{}\begin{matrix}\left(a^2-1\right)\left(b-1\right)\ge0\\\left(b^2-1\right)\left(c-1\right)\ge0\\\left(c^2-1\right)\left(a-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b-b-a^2+1\ge0\\b^2c-c-b^2+1\ge0\\c^2a-a-c^2+1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b\ge a^2+b-1\\b^2c\ge b^2+c-1\\c^2a\ge c^2+a-1\end{matrix}\right.\)
Ta cũng có:
\(2\left(a^3+b^3+c^3\right)\le a^2+b+b^2+c+c^2+a\)
Do đó \(T=2\left(a^3+b^3+c^3\right)-\left(a^2b+b^2c+c^2a\right)\)
\(\le a^2+b+b^2+c+c^2+a\)\(-\left(a^2+b-1+b^2+c-1+c^2+a-1\right)\)
\(=3\)
Vậy GTLN của T=3, đạt được chẳng hạn khi \(a=1;b=0;c=1\)
Đúng 2
Bình luận (1)
cho a,b,c thuộc [0;1]
CMR : a2+b2+c2≤1+a2b+b2c+c2a
Lời giải:
Do $a,b,c\in [0;1]$ nên:
$a^2(1-b)\leq 0$
$b^2(1-c)\leq 0$
$c^2(1-a)\leq 0$
Cộng theo vế suy ra: $a^2+b^2+c^2\leq a^2b+b^2c+c^2a$
Ta có đpcm.
Đúng 2
Bình luận (1)
Phân tích đa thức sau thành nhân tử a 3 + b 3 + c 3 - 3 a b c
Phân tích đa thức thành nhân tử; a^3 +b^3 +b^3 - 3abc
Thay a^3+b^3=(a+b)^3 -3ab(a+b) .Ta có :
Biến đổi vế trái thành:
a^3+b^3+c^3-3abc
<=>(a+b)^3 -3ab(a+b) +c^3 - 3abc
<=>[(a+b)^3 +c^3] -3ab.(a+b+c)
<=>(a+b+c). [(a+b)^2 -c.(a+b)+c^2] -3ab(a+b+c)
<=>(a+b+c).(a^2+2ab+b^2-ca-cb+c^2-3ab
<=>(a+b+c).(a^2+b^2+c^2-ab-bc-ca)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
a) 10x3-90x5
b) 3a2-6a2b+5a-10ab
c) 7a3-28a2+28a
d) 45a3-30a2+5a-500
e) a2b-49b+14b2-b3
f) x4+4