Cho tam giác ABC có \(\widehat{B}>\widehat{C}\), phân giác AD.
a) Chứng minh ADC> ADB và ADC- ADB = B- C
b) So sánh DC và BD.
Những câu hỏi liên quan
Cho tam giác ABC có AB < AC, phân giác AD. Chứng minh :
a, \(\widehat{ADB}\)< \(\widehat{ADC}\)
b, Trên tia AC lấy E sao cho AE=AB. Gọi F là giao điểm của ED và AB. Chứng minh : DF=DC
c,So sánh DB và DC
Cho tam giác ABC có \(\widehat B > \widehat C\). Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh \(\widehat {ADB} < \widehat {ADC}\).
b) Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx} = \widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: \(\Delta ABD = \Delta AED,AB < AC\).
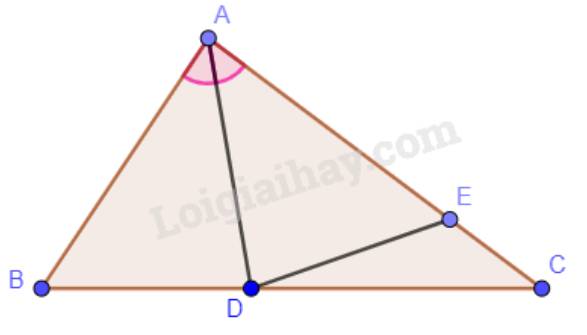
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).
Đúng 0
Bình luận (0)
24 tháng 1 2022 lúc 21:38
Cho tam giác ABC có \(\widehat{A}\)= 60o; \(\widehat{B}\)= 80o và có phân giác AD
a) So sánh các cạnh của tam giác ADC
b) So sánh các cạnh của tam giác ADB
thôi nha mik tự làm đc r
cho Δ ABC . ( AB < AC ) . Đường phân giác AD .
a, Chứng minh \(\widehat{ADB}< \widehat{ADC}\)
b, E ϵ AC sao cho : BE ⊥ AD. chứng minh Δ ABE cân
c, chứng minh BD < CD
a: AB<AC
=>góc B>góc C
góc ADB=góc DAC+góc ACD
góc ADC=góc BAD+góc B
mà góc C<góc B và góc DAC=góc DAB
nên góc ADB<góc ADC
b: Xét ΔAEB có
AD vừa là đường cao, vừa là phân giác
=>ΔAEB can tại A
c: AD là phân giác
=>BD/AB=CD/AC
mà AB<AC
nên BD<CD
Đúng 1
Bình luận (0)
Cho bigtriangleupABC có widehat{ABC} widehat{ACB} và có đường phân giác AD.1) widehat{ADB} và widehat{ADC} là góc ngoài của những tam giác nào? Chứng minh widehat{ADB} widehat{ADC}2) So sánh bigtriangleupABD và bigtriangleupADC
Đọc tiếp
Cho \(\bigtriangleup\)ABC có \(\widehat{ABC}\) = \(\widehat{ACB}\) và có đường phân giác AD.
1) \(\widehat{ADB}\) và \(\widehat{ADC}\) là góc ngoài của những tam giác nào? Chứng minh \(\widehat{ADB} = \widehat{ADC}\)
2) So sánh \(\bigtriangleup\)ABD và \(\bigtriangleup\)ADC
1) \(\widehat{ADB}\) là góc ngoài của t/giác ABC => \(\widehat{ADB}=\widehat{C}+\widehat{DAC}\)
\(\widehat{ADC}\)là góc ngoài của t/giác AD => \(\widehat{ADC}=B+\widehat{DAB}\)
Mà \(\widehat{B}=\widehat{C}\)(gt); \(\widehat{DAB}=\widehat{DAC}\) (gt)
=> \(\widehat{DAB}=\widehat{DAC}\)
2) Xét t/giác ABD và t/giác ADC
có: \(\widehat{BAD}=\widehat{CAD}\) (gt)
AD : chung
\(\widehat{ADB}=\widehat{ADC}\)(cmt)
=> t/giác ABD = t/giác ADC (g.c.g)
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\)có AB < AC và đường phân giác AD . Chứng minh :
a) \(\widehat{ADB}< \widehat{ADC}\)
b) \(DB< DC\)
Xét tam giác ABD và tam giác ACD có :
AB < AC
góc BAD = góc CAD
AD chung
=> tam giác ABD # tam giác ACD
mà AB < AC
=> tam giác ABD < tam giác ACD
=> góc ADB < góc ADC
=> DB < DC
Đúng 0
Bình luận (0)
Tại sao \(\widehat{ADB}< \widehat{ADC}\Rightarrow BD< DC\) ?
Đúng 0
Bình luận (0)
a.hình như trên
Xét tam giác ABD và tam giác ACD có:
Góc ABD =ACD
AC>AB
AD:chung
Do đó tam giác ABD=tam giác ACD
b. Trên tia AC lấy điểm E sao cho AE = AB
=> ∆ = ∆ ADB ADE (c – g – c)
=> BD = ED và góc B^1=góc E^1==>góc B^2=góc E^2
Mà B^2 > góc C (t/c góc ngoài)==>E^2 > góc C => DC > ED
Mà ED = BD nên DC > BD
Xem thêm câu trả lời
Cho tam giác ABC có AB < AC, phân giác AD ( D nằm giữa B,C)
a) chứng minh góc ADB > góc ADC
b) trên AC lấy điểm E sao cho AE = AB. Gọi F là giao điểm của ED và AB. CMR DF = DC
c) so sánh DB và DC
Bài 1: Cho tam giác ABC, AB<AC, phân giác AD . C/m: a/ADB<ADC b/ BD < DC
a: Xét ΔABC có AB<AC
nên góc B>góc C
góc ADB=góc DAC+góc C
góc ADC=góc DAB+góc B
mà góc DAC=góc DAB và góc C<góc B
nên góc ADB<góc ADC
b: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB<AC
nên BD<CD
Đúng 0
Bình luận (0)
cho tam giác ABC có\(\widehat{B}\)=\(\widehat{C}\).Tia phân giác của góc Acắt BC tại D. Chứng minh rằng:
a) tam giác ADB=tam giác ADC
b)AB=AC