Cho tam giác ABC,M là trung điểm của BC.Gọi E là một điểm bất kì trên đoạn AM ,tren tia đối của MA lấy điểm D sao cho MD=ME.Chứng minh CE vuông góc với AB

Những câu hỏi liên quan
Cho tam giác ABC,M là trung điểm của BC.Gọi E là một điểm bất kì trên đoạn AM ,tren tia đối của MA lấy điểm D sao cho MD=ME.Chứng minh CE vuông góc với AB
cho tam giác ABC ,vẽ AH vuông góc với BC .M là trung điểm của BC .trên tia đối của tia của tia HA lấy điểm D sao cho HA=HD.trên tia đối của tia MA lấy điểm E sao cho MA=ME.chứng minh a)tam giác AHB = tam giác DHB b)AB// CE C)BD=CE VẼ HÌNH DÙM MÌNH VỚ...
Xem chi tiết
a) Xét ΔAHB vuông tại H và ΔDHB vuông tại D có
BH chung
AH=DH(gt)
Do đó: ΔAHB=ΔDHB(hai cạnh góc vuông)
b) Xét ΔAMB và ΔEMC có
AM=ME(gt)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔEMC(c-g-c)
⇒\(\widehat{BAM}=\widehat{CEM}\)(hai góc tương ứng)
mà \(\widehat{BAM}\) và \(\widehat{CEM}\) là hai góc ở vị trí so le trong
nên AB//CE(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: ΔABH=ΔDBH(cmt)
nên AB=BD(hai cạnh tương ứng)(1)
Ta có: ΔABM=ΔECM(cmt)
nên AB=CE(hai cạnh tương ứng)(2)
Từ (1) và (2) suy ra BD=CE(đpcm)
Đúng 1
Bình luận (0)
Cho tam giác ABC,M là trung điểm của BC.Gọi E là một điểm bất kì trên đoạn MA,trên tia đối của tia MA lấy điểm D sao cho MD=ME.Chứng minh CE\(\perp\) AB
LÀM NHANH GIÚP MK NHA!!!
Xét tứ giác BECD có
M là trung điểm của BC
Mlà trung điểm của ED
Do đó: BECD là hình bình hành
SUy ra: CE//BD
Đề này chưa đủ dữ kiện để chứng minh CE\(\perp\)AB nhé bạn
Đúng 0
Bình luận (0)
1, Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Vẽ AH vuông góc với BC tại H, trên tia đối của tia HA lấy điểm E sao cho HE = HA. Chứng minh rằng: AE vuông góc với ED.
2, Cho tam giác ABC. Gọi M là trung điểm của BC. Vẽ BD vuông góc với AM tại D, CE vuông góc với AM tại E. Chứng minh rằng : AB + AC > 2AM.
cho tam giác ABC (AB>AC). Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD. a) Chứng minh tam giác ACM= tam giác DBM. b) Kẻ BE vuông góc với AM tại E. Trên tia MD lấy điểm F sao cho M là trung điểm của EF. Chứng minh CF vuông góc với AD. c) Trên tia FB lấy điểm G sao cho B là trung điểm FG. Gọi H là trung điểm của BE. Chứng minh ba điểm G,H,C thẳng hàng
a: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
b: Xét ΔMEB và ΔMFC có
ME=MF
\(\widehat{BME}=\widehat{CMF}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMEB=ΔMFC
=>\(\widehat{MEB}=\widehat{MFC}\)
=>\(\widehat{MFC}=90^0\)
=>CF\(\perp\)AD
c: Xét tứ giác BFCE có
M là trung điểm chung của BC và FE
=>BFCE là hình bình hành
=>BF//CE và BF=CE
Ta có: BF//CE
B\(\in\)FG
Do đó: BG//CE
Ta có: BF=CE
BF=BG
Do đó: BG=CE
Xét tứ giác BGEC có
BG//EC
BG=EC
Do đó: BGEC là hình bình hành
=>BE cắt GC tại trung điểm của mỗi đường
mà H là trung điểm của BE
nên H là trung điểm của GC
=>G,H,C thẳng hàng
Đúng 1
Bình luận (0)
cho tam giác ABC . Gọi M là trung điểm của BC. trên tia đối của tia MA lấy điểm D sao cho MA=MD.
a) Chứng minh tam giác ABM=tam giác DCM và AB///DC
b) Kẻ BE vuông góc với AM( E thuộc AM ), CF vuông góc với DM( F thuộc DM ). Chứng minh: M là trung điểm của EF
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔEMB=ΔFMC
=>EM=FM
=>M là trung điểm của EF
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB = AC. M là trung điểm của BC. Chứng minh:
a. Tam giác ABM = tam giác ACM, AM vuông góc với BC
b. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh: AB//CD
c. Cho ME vuông góc với AB (E thuộc AB), MF vuông góc CD (F thuộc CD). Chứng minh: M là trung điểm của EF. 
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔMBA vuông tại M và ΔMCD vuông tại M có
MB=MC
MA=MD
Do đó: ΔMBA=ΔMCD
=>\(\widehat{MBA}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{MBE}=\widehat{MCF}\)
Do đó: ΔBEM=ΔCFM
=>ME=MF
ΔBEM=ΔCFM
=>\(\widehat{BME}=\widehat{CMF}\)
mà \(\widehat{BME}+\widehat{EMC}=180^0\)(hai góc kề bù)
nên \(\widehat{CMF}+\widehat{EMC}=180^0\)
=>F,M,E thẳng hàng
mà MF=ME
nên M là trung điểm của EF
Đúng 2
Bình luận (0)
Cho tam giác nhọn ABC, M là trung điểm của BC. Đường vuông góc với AB tại B cắt đường thẳng AM tại D. Trên tia MA lấy điểm E sao cho ME = MD. Chứng minh rằng CE vuông góc với AB
+) Xét ΔBMD và ΔCME có:
BM = MC (vì M là trung điểm BC)
MD = ME (giả thiết)
∠BMD = ∠EMC (hai góc đối đỉnh)
⇒ ΔBMD = ΔCME (c.g.c)
⇒ ∠D = ∠MEC (hai góc t.ư)
Mà hai góc này ở vị trí so le trong nên suy ra BD // CE.
Ta có AB ⊥ BD (giả thiết) và BD // CE (chứng minh trên) nên AB ⊥ CE
Đúng 0
Bình luận (0)
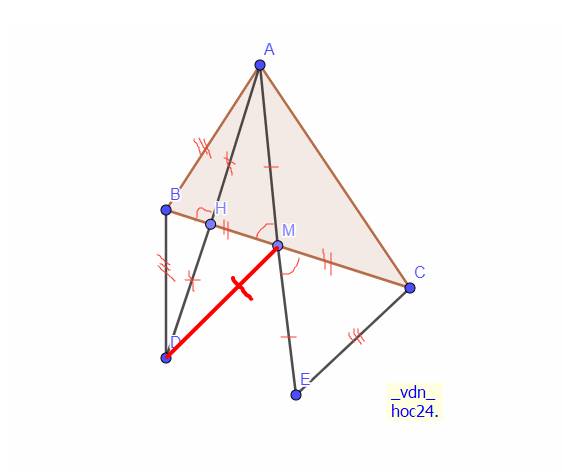
Cho tam giác ABC (AB < AC) M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho AM = EM.
a. Chứng minh: ΔAMB = ΔMCE
b. Từ A kẻ AH vuông góc với BC. Trên tia đối của tia HA lấy điểm D sao cho HA = HD. Chứng minh: CE = BD
c. Tam giác AMD là tam giác gì? Vì sao?
\(\text{#TNam}\)
`a,` Xét Tam giác `AMB` và Tam giác `EMC` có:
`MA=ME (g``t)`
\(\widehat{AMB}=\widehat{CME} (\text {2 góc đối đỉnh})\)
`MB=MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác AMB = Tam giác EMC (c-g-c)}`
`b,` Vì Tam giác `AMB =` Tam giác `EMC (a)`
`-> AB = CE (\text {2 cạnh tương ứng}) (1)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{AHB}=\widehat{DHB}=90^0\)
`\text {BH chung}`
`=> \text {Tam giác ABH = Tam giác DBH (c-g-c)}`
`-> AB = BD (\text {2 cạnh tương ứng}) (2)`
Từ `(1)` và `(2) -> CE = BD.`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`\text {MH chung}`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HA = HD (g``t)`
`=> \text {Tam giác AMH = Tam giác DMH (c-g-c)}`
`-> MA = MD (\text {2 cạnh tương ứng})`
Xét Tam giác `AMD: MA = MD`
`-> \text {Tam giác AMD cân tại M}`
*Hoặc nếu như bạn có học rồi, thì mình có thể dùng cái này cũng được nè cậu:>.
Vì `MH` vừa là đường cao (hạ từ đỉnh `->` cạnh đối diện), vừa là đường trung tuyến.
Theo tính chất của tam giác cân `-> \text {Tam giác AMD là tam giác cân} (đpcm).`
Đúng 1
Bình luận (0)
a: Xét ΔAMB và ΔEMC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔMAD có
MH vừa là đường cao, vừa là trung tuyến
=>ΔMAD cân tại M
Đúng 0
Bình luận (0)
a: Xét ΔMAB và ΔMEC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔMAB=ΔMEC
b: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
=>BA=BD=CE
c: Xét ΔMAD có
MH vừa là đường cao, vừa là trungtuyến
nên ΔMAD cân tại M
Đúng 0
Bình luận (0)


















