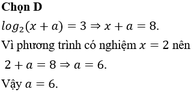Giải phương trình với a là tham số: (x-a)/3 = (x+3)/a - 2

Những câu hỏi liên quan
(1) Cho phương trình bậc hai ẩn x ( m là tham số)x^2-4x+m=0(1) a) Giải phương trình với m =3 b) Tìm đk của m để phương trình (1) luôn có 2 nghiệm phân biệt (2) Cho phương trình bậc hai x^2-2x -3m+1=0 (m là tham số) (2) a) giải pt với m=0 b)Tìm m để pt (2) có nghiệm phân biệt. ( mng oii giúp mk vs mk đang cần gấp:
Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Đúng 1
Bình luận (0)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1
Đúng 1
Bình luận (0)
Giải phương trình với a là tham số
\(\frac{x-a}{3}=\frac{x+3}{a}-2\)
\(\frac{x-a}{3}=\frac{x+3}{a}-2.\) ( a khác 0) (1)
\(\Rightarrow\frac{ax-a^2}{3a}=\frac{3x+9-6a}{3a}\)
=> ax - a2 = 3x + 9-6a
=> ax - 3x = a2 -6a+9
=> x.(a-3) = (a-3)2
nếu a = 3
=> PT vô số nghiệm
nếu \(a\ne3\)
=> x = a-3
nếu a = 3
=> PT vô nghiệm (trái vs đk (1) )
Đúng 0
Bình luận (0)
B1. cho phương trình (x-1)^3-(a^2-a+7)(x-1)-3(a^2-a-2)=0
a, tìm các giá trị của a để một trong các nghiệm là 2
b, giải phương trình với các giá trị đó của a
B2.giải pương trình với tham số a
a, 4ax^3-12x^2-ax+3=0
b, 2a^2x^3+5a^2x^2-8x=20
Bài 2:
a: \(\Leftrightarrow4x^2\left(ax-3\right)-\left(ax-3\right)=0\)
\(\Leftrightarrow\left(ax-3\right)\left(2x-1\right)\left(2x+1\right)=0\)
Trường hợp 1: a=0
=>(2x-1)(2x+1)=0
=>x=1/2 hoặc x=-1/2
Trường hợp 2: a<>0
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\\x=\dfrac{3}{a}\end{matrix}\right.\)
b: \(\Leftrightarrow a^2x^2\left(2x+5\right)-4\left(2x+5\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(a^2x^2-4\right)=0\)
Trường hợp 1: a=0
Phương trình sẽ là 2x+5=0
hay x=-5/2
Trường hợp 2: a<>0
Phương trình sẽ là \(\left(2x+5\right)\left[\left(ax\right)^2-4\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=-\dfrac{2}{a}\\x=\dfrac{2}{a}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho phương trình: xᒾ + 2(m − 1)x+mᒾ - 3 = 0 (1) (m là tham số) a) Giải phương trình (1) với m=2 b) Tìm m để phương trình (1) có hai nghiệm X₁; x₂ thỏa mãn x₁ + x₂ =52
a: Khi m=2 thì (1) sẽ là x^2+2x+1=0
=>x=-1
b:x1+x2=52
=>2m-2=52
=>2m=54
=>m=27
Đúng 0
Bình luận (0)
Cho phương trình ( ẩn x, a là tham số)
\(A=\frac{x+a}{a-x}-\frac{x-a}{a+x}=\frac{a\left(3a+1\right)}{a^2-x^2}\)
a) Giải phương trình với a=-3
b) Giải phương trình khi a=1
c) Tìm các giá trị của a để phương trình nhận x=\(\frac{1}{2}\) là nghiệm
a) ĐKXĐ : \(x\ne\pm a\).
Với \(a=-3\) khi đó ta có pt :
\(A=\frac{x-3}{-3-x}-\frac{x+3}{-3+x}=\frac{-3\left(-9+1\right)}{\left(-3\right)^2-x^2}\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(x+3\right)-\left(x+3\right)\left(-3-x\right)}{\left(-3-x\right)\left(-3+x\right)}+\frac{24}{\left(-3-x\right)\left(-3+x\right)}=0\)
\(\Rightarrow x^2-9-\left(-3x-x^2-9-3x\right)+24=0\)
\(\Leftrightarrow2x^2+6x+24=0\)
\(\Leftrightarrow x^2+3x+12=0\) ( vô nghiệm )
Phần b) tương tự.
\(A=\frac{x+a}{a-x}-\frac{x-a}{a+x}=\frac{a\left(3x+1\right)}{a^2-x^2}\)
\(=\frac{x+a}{a-x}+\frac{x-a}{a+x}=\frac{a\left(3+1\right)}{\left(a-x\right)\left(a+x\right)}\)
\(=\frac{\left(x+a\right)^2+\left(x-a\right)\left(a-x\right)}{\left(a-x\right)\left(a+1\right)}=\frac{a\left(3a+1\right)}{\left(a+x\right)\left(a-x\right)}\)
\(\Leftrightarrow\left(x+a\right)^2+\left(x-a\right)\left(a-x\right)=a\left(3a+1\right)\)
\(\Leftrightarrow x^2+2ax+a^2-ax-x^2-a^2+ax=3a^2+a\)
\(\Leftrightarrow2ax=3a^2+a\)
\(\Leftrightarrow x=\frac{3a^2+a}{2a}\left(a\ne0\right)\)
a) Khi x=-3 => \(x=\frac{3\cdot\left(-3\right)^2-3}{2\left(-3\right)}=-13\)
b) a=1
\(\Leftrightarrow x=\frac{3\cdot1^2+1}{2\cdot1}=2\)
tìm tham số a cho phương trình - 4x - 3 = 4x - 7 nhận x = 2 là nghiệm
Xem thêm câu trả lời
Cho phương trình (ẩn x, a là tham số)
\(A=\frac{x+a}{a-x}-\frac{x-a}{a+x}=\frac{a\left(3a+1\right)}{a^2-x^2}\)
a) Giải phương trình với a=-3
b) Giải phương trình khi a=1
c) Tìm các giá trị của a để phương trình nhận \(x=\frac{1}{2}\)là nghiệm
a) \(ĐKXĐ:x\ne\pm3\)
Với a = -3
\(\Leftrightarrow A=\frac{x-3}{-3-x}-\frac{x+3}{-3+x}=\frac{-3\left[3.\left(-3\right)+1\right]}{\left(-3\right)^2-x^2}\)
\(\Leftrightarrow\frac{3-x}{x+3}-\frac{x+3}{x-3}=\frac{24}{9-x^2}\)
\(\Leftrightarrow\frac{3-x}{x+3}-\frac{x+3}{x-3}+\frac{24}{x^2-9}=0\)
\(\Leftrightarrow\frac{-\left(x-3\right)^2-\left(x+3\right)^2+24}{x^2-9}=0\)
\(\Leftrightarrow-x^2+6x-9-x^2-6x-9+24=0\)
\(\Leftrightarrow-2x^2+6=0\)
\(\Leftrightarrow x^2=3\)
\(\Leftrightarrow x=\pm\sqrt{3}\)(tm)
Vậy với \(a=-3\Leftrightarrow x\in\left\{\sqrt{3};-\sqrt{3}\right\}\)
b) \(ĐKXĐ:x\ne\pm1\)
Với a = 1
\(\Leftrightarrow A=\frac{x+1}{1-x}-\frac{x-1}{1+x}=\frac{3+1}{1-x^2}\)
\(\Leftrightarrow\frac{x+1}{1-x}-\frac{x-1}{1+x}+\frac{4}{x^2-1}=0\)
\(\Leftrightarrow\frac{-\left(x+1\right)^2-\left(x-1\right)^2+4}{x^2-1}=0\)
\(\Leftrightarrow-x^2-2x-1-x^2+2x-1+4=0\)
\(\Leftrightarrow-2x^2+2=0\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow x=\pm1\)(ktm)
Vậy với \(a=1\Leftrightarrow x\in\varnothing\)
c) \(ĐKXĐ:a\ne\pm\frac{1}{2}\)
Thay \(x=\frac{1}{2}\)vào phương trình, ta đươc :
\(A=\frac{\frac{1}{2}+a}{a-\frac{1}{2}}-\frac{\frac{1}{2}-a}{a+\frac{1}{2}}=\frac{a\left(3a+1\right)}{a^2-\frac{1}{4}}\)
\(\Leftrightarrow\frac{a+\frac{1}{2}}{a-\frac{1}{2}}+\frac{a-\frac{1}{2}}{a+\frac{1}{2}}-\frac{3a^2+a}{a^2-\frac{1}{4}}=0\)
\(\Leftrightarrow\frac{\left(a+\frac{1}{2}\right)^2+\left(a-\frac{1}{2}\right)^2-3a^2-a}{a^2-\frac{1}{4}}=0\)
\(\Leftrightarrow a^2+a+\frac{1}{4}+a^2-a+\frac{1}{4}-3a^2-a=0\)
\(\Leftrightarrow-a^2-a+\frac{1}{2}=0\)
\(\Leftrightarrow a^2+a-\frac{1}{2}=0\)
\(\Leftrightarrow\left(a+\frac{1}{2}\right)^2-\frac{3}{4}=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=\frac{\sqrt{3}}{2}-\frac{1}{2}=\frac{\sqrt{3}-1}{2}\\a=-\frac{\sqrt{3}}{2}-\frac{1}{2}=\frac{-\sqrt{3}-1}{2}\end{cases}}\)(TM)
Vậy với \(x=\frac{1}{2}\Leftrightarrow a\in\left\{\frac{\sqrt{3}-1}{2};\frac{-\sqrt{3}-1}{2}\right\}\)
giải phương trình (x - a)/(a + 3) + (x - 3)/(a - 3) = 6a/(9 - a^2) (a là tham số)
Ta có: (x - a)/(a + 3) + (x - 3)/(a - 3) = 6a/(9 - a^2)
<=> (x - a)*(a - 3)/(a^2 - 9) + (x - 3)*(a + 3)/(a^2 - 9)= (-6a)/(a^2 - 9)
=> ax - 3x - a^2 + 3a + ax +3x - 3a - 9 = -6a
<=> 2ax - a^2 + 6a - 9 = 0
<=> 2ax - (a - 3)^2 = 0
<=> 2ax = (a - 3)^2 (1)
Với a=0 thì phương trình (1) vô nghiệm
Với a khác 0 thì
(1) <=> x = (a - 3)^2/2a
Đúng 0
Bình luận (0)
\(ĐKXĐ:\) \(\hept{\begin{cases}a+3\ne0\\a-3\ne0\\9-a^2\ne0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}a\ne-3\\a\ne3\\a\ne\pm3\end{cases}}\)\(\Leftrightarrow\)\(a\ne\pm3\)
\(\frac{x-a}{a+3}+\frac{x-3}{a-3}=\frac{6a}{9-a^2}\)
\(\Leftrightarrow\)\(\frac{\left(x-a\right)\left(a-3\right)}{\left(a+3\right)\left(a-3\right)}+\frac{\left(x-3\right)\left(a+3\right)}{\left(a+3\right)\left(a-3\right)}-\frac{6a}{\left(a+3\right)\left(3-a\right)}=0\)
\(\Leftrightarrow\)\(\frac{ax-3x-a^2+3a+ax+3x-3a-9}{\left(a+3\right)\left(a-3\right)}+\frac{6a}{\left(a+3\right)\left(a-3\right)}=0\)
\(\Leftrightarrow\)\(\frac{-a^2-9+6a}{\left(a+3\right)\left(a-3\right)}=0\)
\(\Leftrightarrow\)\(-\left(a^2-6a+9\right)=0\)
\(\Leftrightarrow\)\(-\left(a-3\right)^2=0\)
\(\Leftrightarrow\)\(a=3\) (vô lý)
Vậy pt vô nghiệm
MK chưa hok giải pt nên ko bít đúng hay sai. P/S tham khảo nha
Đúng 0
Bình luận (0)
Cho phương trình x² – 2(3-m)x-4-m² =0 (x là ẩn, m là tham số) (1). a. Giải phương trình (1) với m = 1. b. Tìm m để phương trình (1) có hai nghiệm phân biệt X₁ , X ₂ thỏa mãn ||x₁ | — |x₂ || =0.
a: Khi m=1 thì (1) sẽ là:
x^2-4x-5=0
=>x=5 hoặc x=-1
Đúng 2
Bình luận (0)
Cho phương trình
log
2
(
x
+
a
)
3
, với a là tham số thực. Biết phương trình có nghiệm x2. Giá trị của a bằng A. 1. B. 10 C. 5 D. 6.
Đọc tiếp
Cho phương trình log 2 ( x + a ) = 3 , với a là tham số thực. Biết phương trình có nghiệm x=2. Giá trị của a bằng
A. 1.
B. 10
C. 5
D. 6.
Giải và biện luận bất phương trình:
a(x-1)/6 + (x-a)/3 > (x+1)/2 (a là tham số)