
Những câu hỏi liên quan
tìm a,b,c,d,e,f biết:
a^2+b^2+c^2+d^2+e^2+f^2+3/7=ab+bc+cd+de+ef+f
Bài 3: Cho hình vẽ bên. Biết DE = 4 cm, D là trung điểm AB, E là trung điểm AC a) Tính BC. b) Gọi M là trung điểm BC. AM cắt DE tại I. Cmr: I là trung điểm DE. c) AM cắt BE tại G. Cmr: IG=1/6 AM
Hình thứ 2 nha
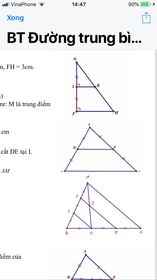
A B C D E 4cm 5cm 6cm x (DE//BC) TÌM X
Đọc tiếp
DE//CB
Theo định lí Ta-lét có:
\(\dfrac{AE}{EC}=\dfrac{AD}{DB}\\ \Rightarrow EC=\dfrac{AE.DB}{AD}\Rightarrow x=\dfrac{5.6}{4}=7,5\)
Đúng 1
Bình luận (1)
Cho góc xAy khác góc bẹt . Lấy 2 điểm B , D thuộc Ax . Lấy 2 điểm C , E thuộc Ay sao cho \(\frac{AD}{BD}=\frac{11}{8}\)và AC = \(\frac{3}{8}\)CE . Cho BC = 6 cm . Chứng minh :
a, BC // DE
b, Tính DE
cm:a) Ta có: \(\frac{AD}{BD}=\frac{11}{8}\)<=> \(\frac{AB+BD}{BD}=\frac{11}{8}\)
<=> \(\frac{AB}{BD}=\frac{11}{8}-1=\frac{3}{8}\)
\(AC=\frac{3}{8}CE\) <=> \(\frac{AC}{CE}=\frac{3}{8}\)
=> \(\frac{AB}{BD}=\frac{AC}{CE}=\frac{3}{8}\)
Theo định lí Ta - lét đảo => BC // DE
b) Do BC // DE, theo định lí Ta - lét, ta có:
\(\frac{AB}{AD}=\frac{BC}{DE}\) <=> \(DE=BC:\left(\frac{AD-BD}{AD}\right)=6:\left(1-\frac{8}{11}\right)=22\left(cm\right)\)
Vậy ....
P = \(\frac{3x-9}{x^2-5x+6}-\frac{x+3}{x-2}-\frac{2x+1}{3-x}.\)
a, Ruts gon
b , Tinh P biet x=-1/2
c, tim x de P < 0
d Tim x e Z de P e Z
a) \(P=\frac{3x-9}{x^2-5x+6}-\frac{x+3}{x-2}-\frac{2x+1}{3-x}\)
\(P=\frac{3\left(x-9\right)}{\left(x-3\right)\left(x-2\right)}-\frac{x+3}{x-2}-\frac{2x+1}{3-x}\)
\(P=\frac{3}{x-2}-\frac{x+3}{x-2}-\frac{2x+1}{3-x}\)
\(P=\frac{3\left(3-x\right)-\left(x+3\right)\left(3-x\right)-\left(2x+1\right)\left(x-2\right)}{\left(x-2\right)\left(3-x\right)}\)
\(P=\frac{9-3x-9+x^2-2x^2+4x-x+2}{\left(x-2\right)\left(3-x\right)}\)
\(P=\frac{2-x^2}{\left(x-2\right)\left(3-x\right)}\) (*)
b) Thay \(x=-\frac{1}{2}\) vào (*) ta có:
\(P=\frac{2-\left(-\frac{1}{2}\right)^2}{\left[\left(-\frac{1}{2}\right)-2\right]\left[3-\left(-\frac{1}{2}\right)\right]}=\frac{2-\frac{1}{4}}{-\frac{5}{2}.\frac{7}{2}}=-\frac{\frac{7}{4}}{\frac{5}{2}.\frac{7}{2}}=-\frac{7}{35}=-\frac{1}{5}\)
c) \(\frac{2-x^2}{\left(x-2\right)\left(3-x\right)}< 0\)
\(\Leftrightarrow2-x^2< 0\)
\(\Leftrightarrow-x^2< -2\)
\(\Leftrightarrow x^2>2\)
\(\Leftrightarrow\hept{\begin{cases}x< -\sqrt{2}\\-\sqrt{2}< x< \sqrt{2}\\x>2\end{cases}}\)
Vậy: ...
Đúng 0
Bình luận (0)
cho hình thang ABCD ( AB//CD và AB < CD) , các cạnh bên AD và BC cắt nhau tại E
a) Tính BC biết AE = 3 , AD = 2 và CE = 6
b) Từ điểm M bất kì trên đáy CD , kẻ MC' // DE và MD' // CE ( C'E , D'E , DE). Chứng minh rằng : DE'/ED + EC'/EC = 1
1.tìm a,b,c,d,e,f biết: a2+b2+c2+d2+e2+f2+3/7=ab+bc+cd+de+ef+f
2.chứng minh: (a+b+c+d)2>=8/3(ab+ac+ad+bc+bd+cd)
m.n giúp mình vs ^^
2/ Ta có \(\left(a+b+c+d\right)^2\ge\frac{8}{3}\left(ab+ac+ad+bc+bd+cd\right)\)
\(\Leftrightarrow a^2+b^2+c^2+d^2+2\left(ab+ac+ad+bc+bd+cd\right)\ge\frac{8}{3}\left(ab+ac+ad+bc+bd+cd\right)\)
\(\Leftrightarrow3\left(a^2+b^2+c^2+d^2\right)+6\left(ab+ac+ad+bc+bd+cd\right)\ge8\left(ab+ac+ad+bc+bd+cd\right)\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2ac+c^2\right)+\left(a^2-2ad+d^2\right)+\left(b^2-2bc+c^2\right)+\left(b^2-2bd+d^2\right)+\left(c^2-2cd+d^2\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(a-d\right)^2+\left(b-c\right)^2+\left(b-d\right)^2+\left(c-d\right)^2\ge0\)(luôn đúng)
Vậy bđt ban đầu được chứng minh.
Đúng 0
Bình luận (0)
lang nha lang nhang cha hieu gi ca
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB<AC. Lấy D thuộc AC; E thuộc AB: góc ADE=góc B. Gọi K;H thứ tự là hình chiếu của E;D trên BC.
a) CMR: AD.AE.BC2=AB+AC+DE2
b) CMR: BE.BA+CD.CA.+HK.BC=BC2
c) Cho biết AB=6 cm; AC=8 cm. Tính DE+EK+DH
Cho tam giác ABC vuông tại A có AB<AC. Lấy D thuộc AC; E thuộc AB: góc ADE=góc B. Gọi K;H thứ tự là hình chiếu của E;D trên BC.
a) CMR: AD.AE.BC2=AB>AC>DE2
b) CMR: BE.BA+CD.CA.+HK.BC=BC2
c) Cho biết AB=6 cm; AC=8 cm. Tính DE+EK+DH
Câu này mk xin sửa lại là AB+AC+DE2 nhé mn
Đúng 0
Bình luận (0)
toán 8.bài 1: tìm gtnn của Ax^2+y^2+xy-5x-4y+2002.bài 2: tính: N75(4^1993+4^1992+...+4^2+5)+25.bài 3: cho tam giác ABC vuông ở A, đường cao AH. gọi D và E lần lượt là hình chiếu của điểm H trên AB,AC.Biết BH4 cm; HC9cm. a/ tính độ dài đoạn DE. B/ chứng mình rằng AB.ADAE.AC. c/ các đường thẳng vuông góc với DE tại D,E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm BH;N là trung điểm của CH. D/ tính diện tích tư giác DENM.bài 4:a/ cho a,b,c0. chứng minh: (a+b+c)(1/a+1/b+1/c)9. b/ cho x+4y5...
Đọc tiếp
toán 8.bài 1: tìm gtnn của A=x^2+y^2+xy-5x-4y+2002.
bài 2: tính: N=75(4^1993+4^1992+...+4^2+5)+25.
bài 3: cho tam giác ABC vuông ở A, đường cao AH. gọi D và E lần lượt là hình chiếu của điểm H trên AB,AC.Biết BH=4 cm; HC=9cm. a/ tính độ dài đoạn DE. B/ chứng mình rằng AB.AD=AE.AC. c/ các đường thẳng vuông góc với DE tại D,E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm BH;N là trung điểm của CH. D/ tính diện tích tư giác DENM.
bài 4:a/ cho a,b,c>0. chứng minh: (a+b+c)(1/a+1/b+1/c)>=9. b/ cho x+4y=5. tìm gtnn của M=4x^2+4y^2
. bài 5: chứng minh: x^4+x^3+x^2+x+1 >0.
bài 6: giải pt: | |x|-3 |=x+1 (2 dấu giá trị tuyệt đối nhé.)
mình đc 4a à
(a+b+c)(1/a+1/b+1/c)=1+a/b+a/c+b/a+1+b/c+c/a+c/b+1=3+(a/b+b/a)+(a/c+c/a)+(b/c+c/b)
mà a/b+b/a>=2(BĐT cosi)
cmtt ta đc
3+2+2+2>=9
Vậy(a+b+c)(1/a+1/b+1/c)>=9
Đúng 0
Bình luận (0)


















