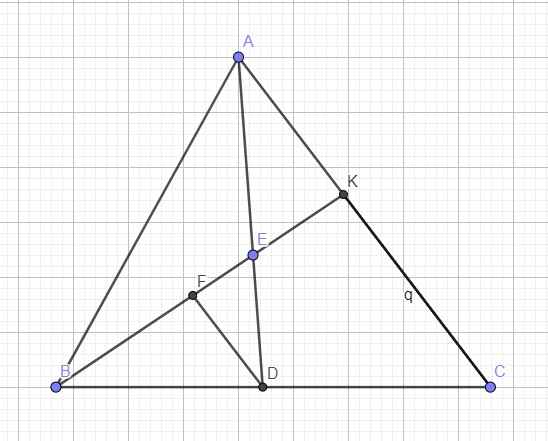
cho tam giác ABC, có Ab= 16cm, ac=24cm, đường phân giác AD. Điểm E thuộc đoạn thẳng AD sao cho AE=3/5AD. Gọi K là gd của BE và AC. Tính AK,KC

Những câu hỏi liên quan
Cho △ABC, AB= 16cm, AC= 24cm, đường phân giác AD. Điểm E thuộc đoạn
thẳng AD sao cho AE = \(\dfrac{3}{5}\) AD . Gọi K là giao điểm của BE và AC. Tính độ dài AK, KC.
Áp dụng định lý phân giác:
\(\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{2}{3}\Rightarrow3BD=2CD=2\left(BC-BD\right)\)
\(\Leftrightarrow5BD=2BC\Rightarrow BD=\dfrac{2}{5}BC\Rightarrow\dfrac{BD}{BC}=\dfrac{2}{5}\)
\(AE=\dfrac{3}{5}AD=\dfrac{3}{5}\left(AE+DE\right)\Rightarrow2AE=3DE\Rightarrow\dfrac{DE}{AE}=\dfrac{2}{3}\)
Qua D kẻ đường thẳng song song AC cắt AE tại F
Áp dụng định lý Talet:
\(\dfrac{FD}{AK}=\dfrac{FE}{KE}=\dfrac{DE}{AE}=\dfrac{2}{3}\)
Talet cho tam giác BCK: \(\dfrac{FD}{CK}=\dfrac{BD}{BC}=\dfrac{2}{5}\)
\(\Rightarrow\left(\dfrac{FD}{AK}\right):\left(\dfrac{FD}{CK}\right)=\left(\dfrac{2}{3}\right):\left(\dfrac{2}{5}\right)\Leftrightarrow\dfrac{CK}{AK}=\dfrac{5}{3}\)
\(\Rightarrow\dfrac{CK}{AC-CK}=\dfrac{5}{3}\Rightarrow3CK=5\left(24-CK\right)\Rightarrow CK=15\)
\(AK=AC-CK=9\)
Đúng 2
Bình luận (0)
cho tam giác ABC có AB=16cm,AC=24cm, đường phân giác AD.điểm E thuộc AD sao cho AE=3/5AD.gọi K là giao điểm của BE và AC . tính ak,kc
cho tam giac ABC AB 16 AC 24. đường phân giác AD điểm E thuộc AD sao cho gọi K là giao điểm của BE và AC tính AK, KC
Áp dụng định lý phân giác:
⇔5BD=2BC⇒BD=25BC⇒BDBC=25⇔5BD=2BC⇒BD=25BC⇒BDBC=25
FDAK=FEKE=DEAE=23FDAK=FEKE=DEAE=23
Talet cho tam giác BCK: ⇒(FDAK):(FDCK)=(23):(25)⇔CKAK=53⇒(FDAK):(FDCK)=(23):(25)⇔CKAK=53
Đúng 0
Bình luận (0)
cho tam giac ABC;AB=16;AC=24. đường phân giác AD điểm E thuộc AD sao cho gọi K là giao điểm của BE và AC tính AK, KC
cho tam giác ABC ,lấy điểm D trên cạh BC sao cho BD=3/4BC.điểm E trên đoạn thẳng AD sao cho AE=1/3 AD Gọi K là giao điểm BE Và Ac tính tỉ số AK/KC
1 Cho tam giác ABC có AD=AE=BE, gọi M là trung điểm BC. Gọi K là điểm thuộc cạnh AC sao cho AK=1/3AC. CMR B,I,K thẳng hàng
2 Cho tam giác ABC có AD=AE=BE, gọi M là trung điểm BC, D,K lần lượt thuộc AB,AC sao cho AD=1/3 AB, AK=1/3 AC. CMR 3 đường thẳng AM, BK, CI đồng vị
Cho tam giác ABC và điểm D trên cạnh BC sao cho BD/BC = 3/4, điểm E trên đoạn AD sao cho AE/AD = 1/3. Gọi K là giao điểm của BE và AC. Tính tỉ số AK/KC
Cho tam giác BD=3/4 BC .Điểm E trên Ad sao cho AE =1/3 AD Gọi K là giao điểm của BE và AC Tính AK/KC.
Kẻ DH//BK , H thuộc AC)
Cho tam giác ABC có AB < AC và tia phân giác AD. TRên tia AC lấy E sao cho AE = AB
a) CMR: BD = DE
b) Gọi K là giao điểm của đường thẳng AB và ED. CMR: tam giác DBK = tam giác DEC.
c) Tam giác AKC là tam giác gì?
d) CMR: AD vuông góc KC.
hình tự vẽ
a)Vì AD là tpg của ^BAC
=>^BAD = ^CAD = ^BAC/2
Xét tam giác ABD và tam giác AED có:
AD:cạnh chung
^BAD=^CAD(cmt)
AB=AE(gt)
=>tam giác ABD=tam giác AED (c.g.c)
=>BD=BE (cặp cạnh t.ư)
b)Vì tam giác ABD=tam giác AED(cmt)
=>^ABD=^AED (cặp góc t.ư)
Ta có:^ABD+^KBD=1800 (kề bù)
=>^KBD=1800-^ABD (1)
^AED+^CED=1800 (kề bù)
=>^CED=1800-^AED(2)
Từ (1);(2);có ^ABD=^AED(cmt)
=>^KBD=^CED
Xét tam giác DBK và tam giác DEC có:
BD=BE(cmt
^KBD=^CED(cmt)
^BDK=^EDC (2 góc đđ)
=>tam giác DBK=tam giác DEC (g.c.g)
Đúng 1
Bình luận (0)
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: BD=ED
b: Xét ΔDBK và ΔDEC có
\(\widehat{DBK}=\widehat{DEC}\)
BD=ED
\(\widehat{BDK}=\widehat{EDC}\)
Do đó: ΔDBK=ΔDEC
c: Ta có: ΔDBK=ΔDEC
nên BK=EC
Ta có: AB+BK=AK
AE+EC=AC
mà AB=AE
và BK=EC
nên AK=AC
hay ΔAKC cân tại A
Đúng 1
Bình luận (0)