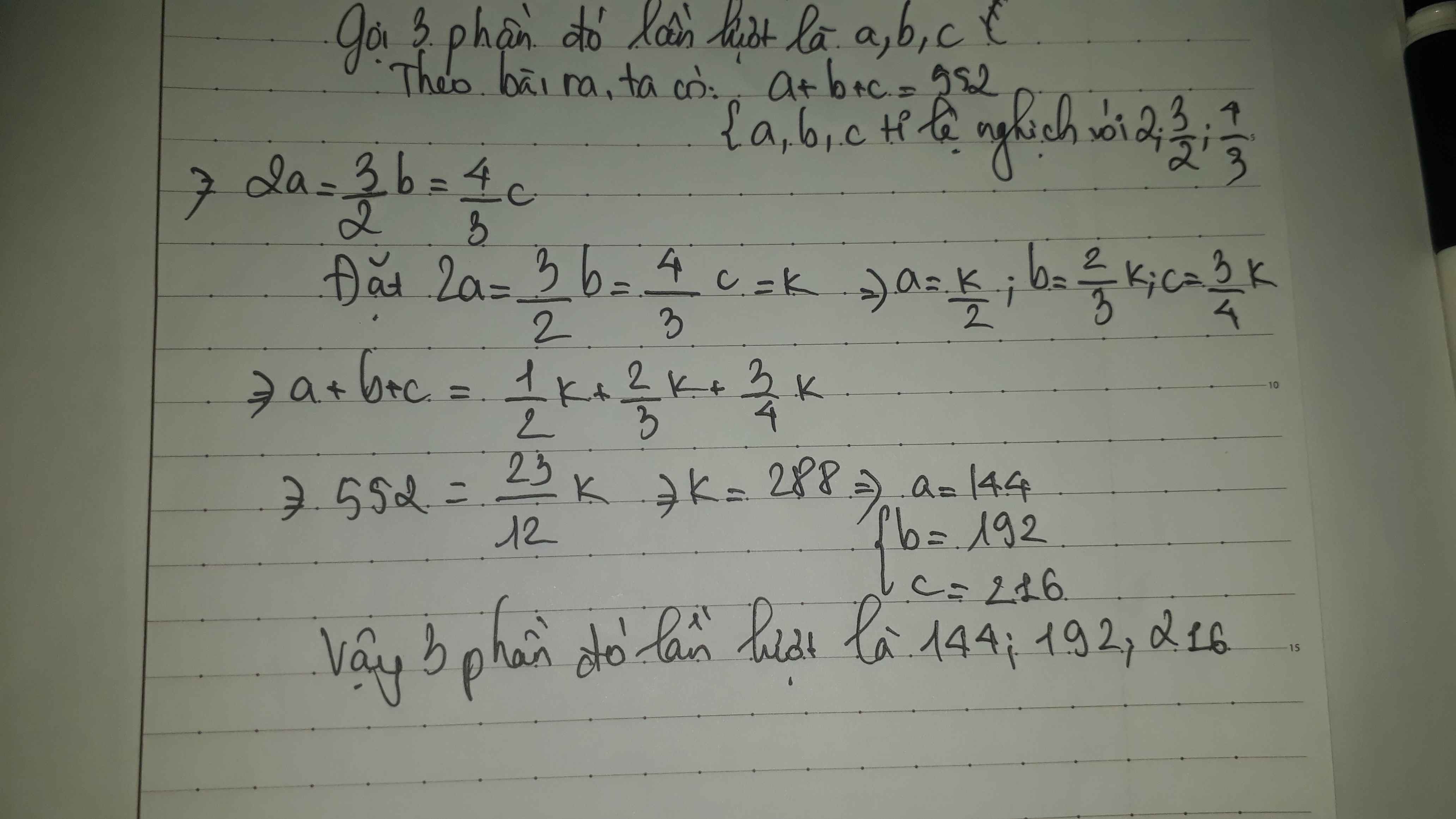Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{2}{3}}=\dfrac{c}{\dfrac{3}{4}}=\dfrac{a+b+c}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}}=\dfrac{69}{\dfrac{23}{12}}=36\)

Do đó: a=18; b=24; c=27

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{2}{3}}=\dfrac{c}{\dfrac{3}{4}}=\dfrac{a+b+c}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}}=\dfrac{69}{\dfrac{23}{12}}=36\)

Do đó: a=18; b=24; c=27

Gọi ba phần cần tìm lần lượt là a,b,c

Theo đề, ta có: \(\dfrac{1}{5}a=\dfrac{10}{3}b=\dfrac{4}{5}c\)

=>\(\dfrac{a}{5}=\dfrac{b}{\dfrac{5}{4}}=\dfrac{c}{\dfrac{3}{10}}\)

Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{a}{5}=\dfrac{b}{\dfrac{5}{4}}=\dfrac{c}{\dfrac{3}{10}}=\dfrac{a+b+c}{5+\dfrac{5}{4}+\dfrac{3}{10}}=\dfrac{786}{\dfrac{131}{20}}=120\)

=>a=600; b=150; c=36

Gọi 3 phần được chia là \(x;y;z\)

Theo đề bài ta có:

\(\dfrac{1}{5}x=1\dfrac{1}{4}y=0,03z\)

\(\Rightarrow\dfrac{1}{5}x=\dfrac{5}{4}y=\dfrac{3}{100}z\)

\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{\dfrac{4}{5}}=\dfrac{z}{\dfrac{100}{3}}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{5}=\dfrac{y}{\dfrac{4}{5}}=\dfrac{z}{\dfrac{100}{3}}\)

\(=\dfrac{x+y+z}{5+\dfrac{4}{5}+\dfrac{100}{3}}\)

\(=\dfrac{980}{\dfrac{587}{15}}=25...\)

....

Gọi 3 phân số cần tìm là a , b , c .

Vì mẫu số tỉ lệ nghịch với \(\dfrac{1}{4}\),\(\dfrac{1}{5}\),\(\dfrac{1}{6}\) nên sẽ tỉ lệ thuận với 4;5;6

=>a:b:c = \(\dfrac{5}{4}\):\(\dfrac{7}{5}\):\(\dfrac{11}{6}\) = \(\dfrac{5}{4}\).60 : \(\dfrac{7}{5}\).60 : \(\dfrac{11}{6}\).60 = 75:84:110

=>\(\dfrac{a}{75}\)=\(\dfrac{b}{84}\)=\(\dfrac{c}{110}\)

Vì tổng của chúng là\(15\dfrac{83}{120}\) nên a+b+c = \(15\dfrac{83}{120}\)=1883

Áp dụng tính chất của dãy tỉ số bằng nhau ta có :

\(\dfrac{a}{75}\)=\(\dfrac{b}{84}\)=\(\dfrac{c}{110}\)=\(\dfrac{a+b+c}{75+84+110}\)=\(\dfrac{1883}{269}\)=7

\(\dfrac{a}{75}\)=7 => a = 75.7 = 525

\(\dfrac{b}{84}\)=7 => b = 84.7 = 588

\(\dfrac{c}{110}\)=7 => c = 110.7 = 770

Vậy 3 phân số tối giản cần tìm là 525 ; 585 ; 770 .

Gọi 3 phân số cần tìm là \(\frac{a}{b};\frac{c}{d};\frac{e}{f}\)

Theo đề bài ta có:

\(\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=15\frac{83}{120}=\frac{1883}{120}\) (1)

\(a\div c\div e=5\div7\div11\Leftrightarrow\frac{a}{5}=\frac{c}{7}=\frac{e}{11}\)

Đặt các tỉ số trên là \(p\)

\(\Rightarrow\left\{\begin{matrix}a=5p\\b=7p\\c=11p\end{matrix}\right.\) (2)

\(b\div d\div f=\frac{1}{\frac{1}{4}}\div\frac{1}{\frac{1}{5}}\div\frac{1}{\frac{1}{6}}=4\div5\div6\Leftrightarrow\frac{b}{4}=\frac{d}{5}=\frac{f}{6}\)

Đặt các tỉ số trên là \(q\)

\(\Rightarrow\left\{\begin{matrix}b=4q\\d=5q\\f=6q\end{matrix}\right.\) (3)

Từ (1);(2) và (3)

\(\Rightarrow\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=\frac{5p}{4q}+\frac{7p}{5q}+\frac{11p}{6q}=\frac{1883}{120}\)

\(\Rightarrow\frac{5}{4}.\frac{p}{q}+\frac{7}{5}.\frac{p}{q}+\frac{11}{6}.\frac{p}{q}=\frac{p}{q}\left(\frac{5}{4}+\frac{7}{5}+\frac{11}{6}\right)=\frac{1883}{120}\)

\(\Rightarrow\frac{269}{60}.\frac{p}{q}=\frac{1883}{120}\Rightarrow\frac{p}{q}=\frac{7}{2}\)

\(\Rightarrow\left\{\begin{matrix}\frac{a}{b}=\frac{5}{4}.\frac{7}{2}=\frac{35}{8}\\\frac{c}{d}=\frac{7}{5}.\frac{7}{2}=\frac{49}{10}\\\frac{e}{f}=\frac{11}{6}.\frac{7}{2}=\frac{77}{12}\end{matrix}\right.\)

Vậy 3 phân số đó là: \(\left\{\begin{matrix}\frac{35}{8}\\\frac{49}{10}\\\frac{77}{12}\end{matrix}\right.\)

Gọi 3 phần cần tìm là \(x,y,z\)

Theo đề bài ta có:

\(x+y+z=980\) và \(x:y:z=\dfrac{1}{5}:1\dfrac{1}{4}:0,3\)

Biến đổi tỉ số giữa các phân số thành tỉ số giữa các số nguyên, ta có:

\(\dfrac{1}{5}:1\dfrac{1}{4}:0,3=\dfrac{1}{5}:\dfrac{5}{4}:\dfrac{3}{10}=\dfrac{4}{20}:\dfrac{25}{20}:\dfrac{6}{20}\)

Do đó: \(\dfrac{x}{4}=\dfrac{y}{25}=\dfrac{z}{6}=\dfrac{x+y+z}{4+25+6}=\dfrac{980}{35}=28\)

Vậy \(\left\{{}\begin{matrix}x=28.4=112\\y=28.25=700\\z=28.6=168\end{matrix}\right.\)

Chết! Nhầm 0,03 thành 0,3 rồi.

Ngân Hà làm vậy đúng rồi, mình chép nhầm đề bài từ 0,3 thành 0,03