Cho tam giác \(ABC\) nội tiếp đường tròn \(\left(O\right)\), đường cao \(AH\) (\(H\in BC\)), AH cắt đường tròn ở \(E\).
a) So sánh: \(\widehat{BAH}\) và \(\widehat{OAC}\)
b) Tứ giác \(BCED\) là hình gì?
cho tam giác ABC (AB<AC), nội tiếp đường tròn tâm (O) ,đường cao AH (H thuộc Bc) ,AH cắt đường tròn ở P ,AO cắt đường tròn ở E .
a) So sánh hai góc BAH và góc OAC
b) Tứ giác BCED là hình gì?
giúp em với ạ :(((
cho tam giác abc (ab<ac ) nội tiếp đường tròn tâm o , đường cao ah , ah cắt đường tròn ở d , ao cắt đường tròn ở e. chứng minh góc bah = góc oac , tứ giác bced là hình gì ?
a, ABDC nội tiếp
=> ˆBAH = ˆBCD
ACED nội tiếp
=> OAC^ = CDE^
Lại có ΔDEA nội tiếp đường tròn đường kínhAE
=> DE ⊥ AD
mà AD ⊥ BC
=> DE // BC=>BCD^ =CDE^ ( so le trong)
=>BAH^ = OAC^
b, DE // BC=> BDEC là hình thang (*)
Lại có:
DBC^ = DAC^ ( BDAC nội tiếp) (1)
BCE^= EAB^ ( ABEC nội tiếp) (2)
Lại có: BAH^ = OAC^
=> BAH^ + HAO^ = OAC^ + ˆHAO
=> EAB^ = DAC^ (3)
Từ (1) (2) (3) => DBC^= BCE^ (**)
từ (*) và (**) => BCED là hình thang cân
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Từ đỉnh A ta kẻ đường cao AH (H $\in$ BC). Chứng minh rằng $\widehat{BAH}=\widehat{OAC}$.
Vẽ đường kính AK
+) Dễ có: ^KBC = ^KAC (2 góc nội tiếp cùng chắn cung KC) (1)
+) ^ABK là góc nội tiếp chắn nửa đường tròn nên ^ABK = 900
Có: ^KBC + ^CBA = ^ABK = 900 (cmt)
^BAH + ^CBA = 900 (∆ABH vuông tại H)
Từ đó suy ra ^KBC = ^BAH (2)
Từ (1) và (2) suy ra ^BAH = ^KAC hay ^BAH = ^OAC (đpcm)
Kẻ đường kính AE của đường tròn ( O) . Ta thấy \(\widehat{ACE}=90^o\)( góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow\widehat{OAC}+\widehat{AEC}=90^o\) (1)
Theo gt, ta có: \(\widehat{BAH}+\widehat{ABC}=90^O\) (2)
Lại có: \(\widehat{AEC}=\widehat{ABC}\) (3)
Từ (1), (2), (3) => đpcm
có AEC = ABC ( góc nội tiếp chắn cung AC)
mà AHB = AEC ( =90 độ )
nên tam giác ABH ~ tam giác AEC
=> BAH = EAC=OAC
Cho tam giác ABC (AB<AC) nội tiếp đt(O), đường cao AH (H thuộc BC ). AH cắt đt ở D, AD cắt đt ở E.
a) So sánh 2 góc BAH và DAC.
b) Tứ giác BCED là hình gì ? Vì sao?
Giả sử ABC là tam giác nhọn nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:
a, BC song song với DE
b, Tứ giác BCED là hình thang cân
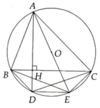
a, HS tự chứng minh
b, Ta chứng minh được B E ⏜ = C D ⏜ từ đó suy ra BE = CD và tứ giác BDEC là hình thang cân
Cho \(\Delta ABC\) nhọn (AB<AC) nội tiếp đường tròn (O). các đường cao BE, CF cắt nhau tại H. Gọi D là giao điểm của AH và BC. Tiếp tuyến tại A của (O) cắt BC tại F
a) Chứng minh tứ giác AEHF nội tiếp và \(\widehat{EAH}=\widehat{EBC}\)
b) Đường kính AK của (O) cắt EF tại M, cắt BC tại N. Tiếp tuyến tại K của (O) cắt AH tại Q. Chứng minh HM // QN
c) Gọi I là trung điểm BC. Đường tròn đường kính AH cắt AI tại P. Chứng minh SA = SP
a: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
góc EAH+góc ACB=90 độ
góc EBC+góc ACB=90 độ
=>góc EAH=góc EBC
b: AK cắt EF tại M
AK cắt BC tại N
AH cắt (O) tại K
=>HM//AB và QN//AB
=>HM//QN
cho tam giác ABC nội tiếp đường tròn , kẻ đường cao AH của tam giác và đường kính AD của đường tròn . Chứng ,minh rằng \(\widehat{BAH}=\widehat{DAC}\)
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{ADC}\)(Hệ quả góc nội tiếp)
hay \(\widehat{ABH}=\widehat{ADC}\)(1)
Xét (O) có
ΔADC nội tiếp đường tròn(A,D,C∈(O))
AD là đường kính(gt)
Do đó: ΔADC vuông tại C(Định lí)
Suy ra: \(\widehat{DAC}+\widehat{ADC}=90^0\)(Hai góc nhọn phụ nhau)(2)
Ta có: ΔABH vuông tại H(AH⊥BC)
nên \(\widehat{BAH}+\widehat{ABH}=90^0\)(Hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{BAH}=\widehat{DAC}\)(đpcm)
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:
a) BC // DE.
b) Tứ giác BCED là hình thang cân.
a) Từ O kẻ OM vuông góc với AD
Khi đó theo tính chất của đường kính và dây cung thì M là trung điểm AD
Lại có O là trung điểm AE => MO là đường trung bình của tam giác ADE
=> MO // DE , lại có MO // BC (cùng vuông góc với AD)
=> DE // BC
b) Tứ giác ABDC nột tiếp đường tròn (O)
=> \(\widehat{ADB}=\widehat{BCA}\Leftrightarrow90^0-\widehat{ADB}=90^0-\widehat{BCA}\Rightarrow\widehat{CBD}=\widehat{ECB}\)
Lại có từ phần a, BED là hình thang vì có BC // DE
=> BCED là hình thang cân

a, Xét ΔADE nội tiếp đường tròn đường kính AE
=> AD ⊥ DE (1)
LẠi có AH ⊥ BC = > AD ⊥ BC (2)
Từ (1) và (2) => DE // BC ( cùng vuông góc với AD) (*)
b, Ta có: Tứ giác ABDC nội tiếp
=> =
Lại có : + = + ( cùng bằng 90 độ)
=> = (**)
Từ (*) và (**) => BCED là hình thang cân
a) Xét (O) có : AE đường kính (GT) và D ϵ (O) ⇒ Δ ADC vuông tại D
⇒ AD vuông góc với DE tại D. Mà BC vuông góc với AD tại H (GT)
⇒ BC // DE ( theo định lí từ vuông góc đên song song )
b) CM dễ dàng △ AEC vuông tại C.
Xét (O) có : góc DBC = góc DAC ( vì 2 góc nội tiếp cùng chắn cung CD ) (1)
Mà góc DAC + góc ACB = 90 độ ( △AHC vuông tại H )
góc BCE + góc ACB = 90 độ ( △AEC vuông tại C )
⇒ góc DAC = góc BCE (2)
Từ (1) và (2) ⇒ góc DBC = góc BCE.
Xét hình thang BCED (vì BC // ED) có ; góc DBC = góc BCE (cmt)
⇒ BCED là hình thang cân,
Cho tam giác ABC có ba góc nhọn nội tiếp (O;R) đường cao AH của tam giác cắt đường tròn tâm O tại D . Từ D vẽ đường thẳng song song với BC cắt đường tròn O tại E .CM : BCED là hình thang cân