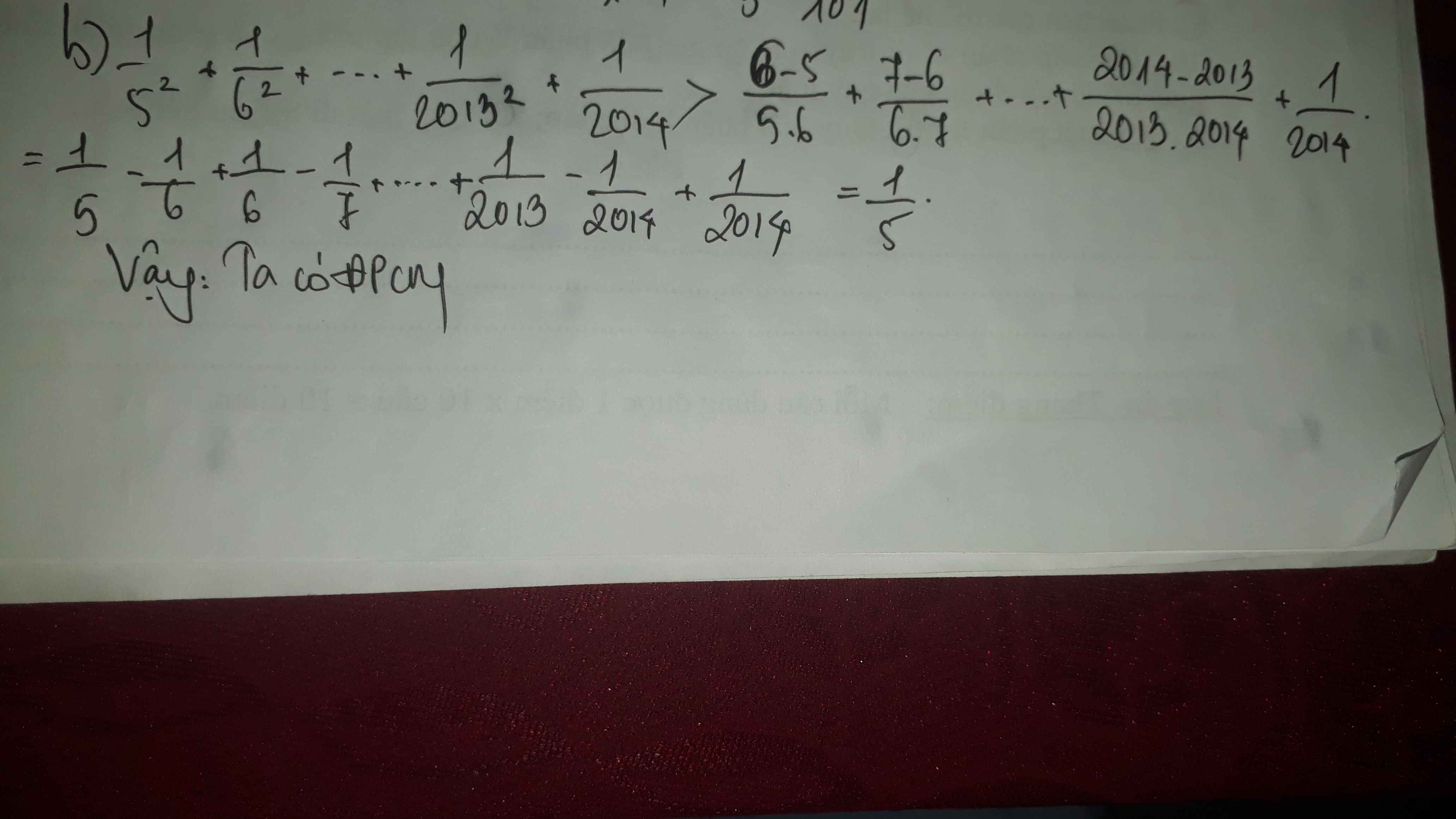Ai trả lời đi please

A= 1+(\(\dfrac{1}{2014}\)+1)+(\(\dfrac{2}{2013}\)+1)+...+(\(\dfrac{2013}{2}\)+1)

= \(\dfrac{2015}{2015}\)+(\(\dfrac{1}{2014}\)+1)+(\(\dfrac{2}{2013}\)+1)+...+(\(\dfrac{2013}{2}\)+1)

= 2015.(\(\dfrac{1}{2015}\)+\(\dfrac{1}{2014}\)+\(\dfrac{1}{2013}\)+...+\(\dfrac{1}{2}\))=2015.B

\(\Rightarrow\) \(\dfrac{A}{B}\)=2015

https://hoc24.vn/hoi-dap/question/598367.html

khó quá

Không ai trả lời đc đành phải tự trả lời thôi :))

A=1/2! - 2/3! - 3/4! - .... - 2013/2014!

=1/2! - (2/3! + 3/4! +...+ 2013/2014!)

= 1/2! - [(3-1)/3! + (4-1)/4!+(4-1)/5! + ... + (2014-1)/2014!]

=1/2! - [(3/3! + 4/4! + ...+ 2014/2014!) - (1/3! + 1/4! +... + 1/2013! + 1/2014!)] 

Ta có: Với n là số nguyên dương, n>2
\(\dfrac{n}{n!}\)=\(\dfrac{n}{1....\left(n-1\right)\left(n\right)}=\dfrac{1}{1.2....\left(n-1\right)}=\dfrac{1}{\left(n-1\right)!}\)

Do đó

A=1/2! - [ (1/2! + 1/3! + ... + 1/2013!) - (1/3!+ 1/4! +... + 1/2013! + 1/2014!) ]

= 1/2! - (1/2! - 1/2014!)

= 1/2014!

Vậy đáp án là A = \(\dfrac{1}{2014!}\)

\(A=\dfrac{\dfrac{1}{2013}+\dfrac{2}{2012}+\dfrac{3}{2011}+...+\dfrac{2011}{3}+\dfrac{2012}{2}+\dfrac{2013}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2014}}\)

\(A=\dfrac{1+\left(\dfrac{1}{2013}+1\right)+\left(\dfrac{2}{2012}+1\right)+\left(\dfrac{3}{2011}+1\right)+...+\left(\dfrac{2012}{2}+1\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2014}}\)

\(A=\dfrac{\dfrac{2014}{2014}+\dfrac{204}{2013}+\dfrac{2014}{2012}+\dfrac{2014}{2011}+...+\dfrac{2014}{2}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2014}}\)

\(A=\dfrac{2014\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2014}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2014}}=2014\)

mình ko chắc đúng nha !

Số số hạng của tử là :

(2013-1):1+1=2013(số hạng)

\(\dfrac{\dfrac{1}{2013}+\dfrac{2}{2012}+\dfrac{3}{2011}+.....+\dfrac{2011}{3}+\dfrac{2012}{2}+\dfrac{2013}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{2013}+\dfrac{1}{2014}}\)

\(=\dfrac{\dfrac{1}{2013}+1+\dfrac{2}{2012}+1+....+\dfrac{2012}{2}+1+\dfrac{2013}{1}-2012}{\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{2013}+\dfrac{1}{2014}}\)

\(=\dfrac{\dfrac{2014}{2013}+\dfrac{2014}{2012}+....+\dfrac{2014}{2}+1}{\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{2013}+\dfrac{1}{2014}}\)

\(=2014\left(\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{2013}+\dfrac{1}{2014}}{\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{2013}+\dfrac{1}{2014}}\right)\)

=2014

Mình ghi thêm ở cái dâu bằng thứ 2 cuối cùng trên tử có ghi trừ 2012 là do tử có 2013 hạng tử mà mình chỉ cộng 1 cho 2012 hạng tử nên phải trừ đi 2012

Câu này mình từng làm qua (tuy khác đề) nhưng bạn chỉ cần áp dụng đúng công thức là OK nhé: https://olm.vn/hoi-dap/question/1294056.html

\(A=1+\dfrac{\dfrac{\left(1+2\right).2}{2}}{2}+\dfrac{\dfrac{\left(1+3\right).3}{2}}{3}+...+\dfrac{\dfrac{\left(1+2013\right).2013}{2}}{2013}\)

\(A=1+\dfrac{\dfrac{3.2}{2}}{2}+\dfrac{\dfrac{4.3}{2}}{3}+...+\dfrac{\dfrac{2014.2013}{2}}{2013}\)

\(A=1+\dfrac{3}{2}+\dfrac{2.3}{3}+...+\dfrac{1007.2013}{2013}\)

\(A=1+\dfrac{3}{2}+2+\dfrac{5}{2}...+1007\)

\(2A=2+3+4+5+6+...+2012+2013+2014\)

\(2A=\dfrac{\left(2+2014\right).2013}{2}\)

\(A=\dfrac{2016.2013}{4}=504.2013\)

\(B=\dfrac{-2}{1.3}+\dfrac{-2}{2.4}+...+\dfrac{-2}{2012.2014}+\dfrac{-2}{2013.2015}\)

\(-B=\dfrac{2}{1.3}+\dfrac{2}{2.4}+...+\dfrac{2}{2012.2014}+\dfrac{2}{2013.2015}\)

\(-B=\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{2013.2015}\right)+\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{2012.2014}\right)\)

\(-B=\left(\dfrac{3-1}{1.3}+\dfrac{5-3}{3.5}+...+\dfrac{2015-2013}{2013.2015}\right)+\left(\dfrac{4-2}{2.4}+\dfrac{6-4}{4.6}+...+\dfrac{2014-2012}{2012.2014}\right)\)

\(-B=\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{2013}-\dfrac{1}{2015}\right)+\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}+...+\dfrac{1}{2012}-\dfrac{1}{2014}\right)\)

\(-B=\left(1-\dfrac{1}{2015}\right)+\left(\dfrac{1}{2}-\dfrac{1}{2014}\right)\)

\(-B=\dfrac{2014}{2015}+\dfrac{2012}{2014.2}=\dfrac{2014^2+1006.2015}{2015.2014}\)

\(B=\dfrac{2014^2+1006.2015}{-2015.2014}\)