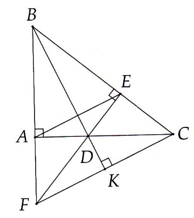
Cho tam giác ABC biết AB < AC . Trên tia BA lấy điểm D sao cho BD = BC. T ia phân giác góc ABC cắt CD tại E .
a) C/m tam giác BED = tam giác BEC b) BE cắt AC tại K . C/m tam giác CKD cân
c) Vẽ AH // BE ( H thuộc CD ) . C/m AH vuông góc CD . d) C/m 2AD + AB > AH + BE