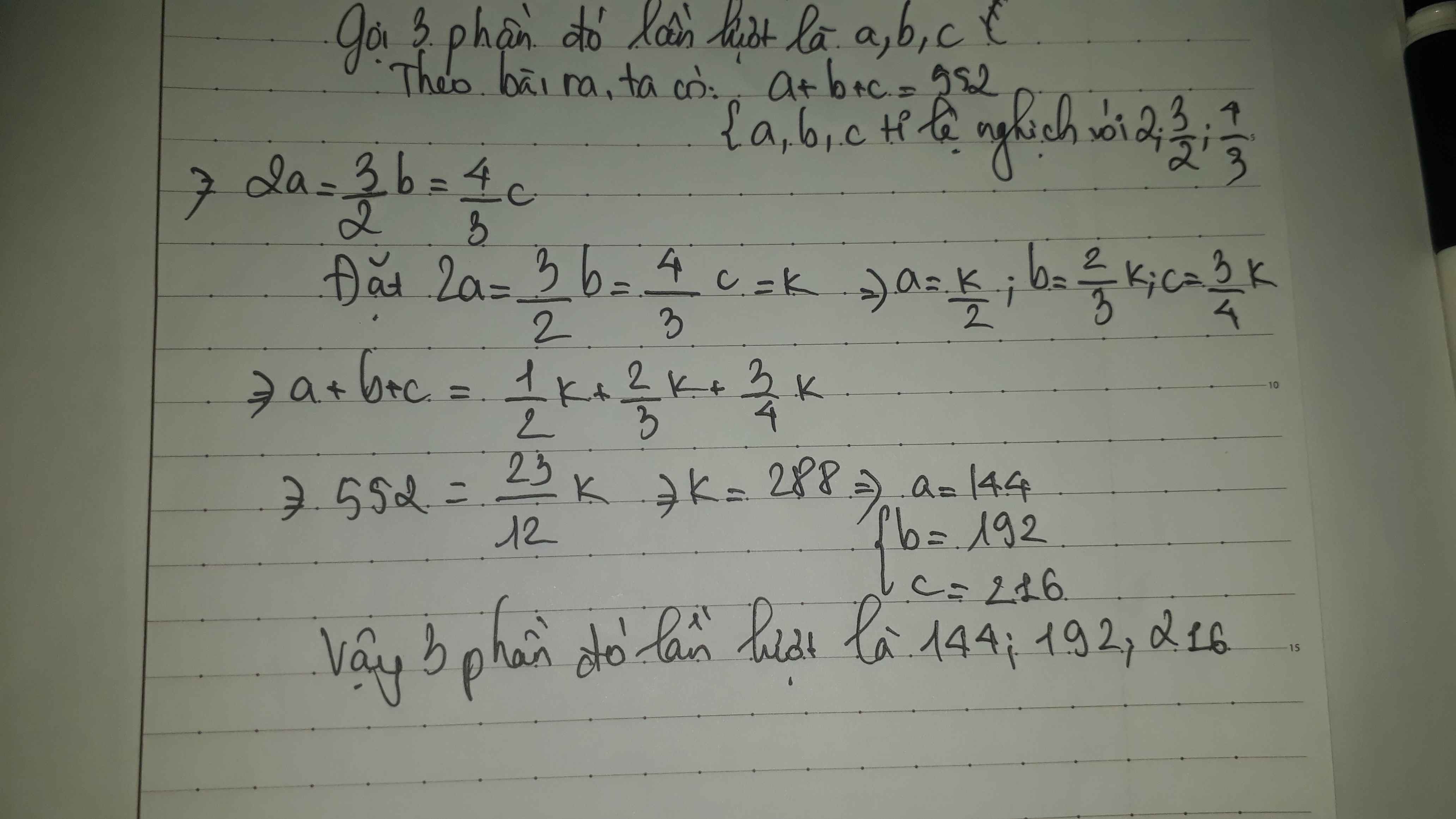Chia số 552 thành 3 phần tỉ lệ với \(\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{4}\)

Những câu hỏi liên quan
chia số 552 thành 3 phần tỉ lệ nghịch với 2; \(\dfrac{3}{2}\); \(\dfrac{4}{3}\)
tìm 3 phần đó
Chia số 69 thành ba phần tỉ lệ với các số \(\dfrac{1}{2};\dfrac{2}{3}\) và \(\dfrac{3}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{2}{3}}=\dfrac{c}{\dfrac{3}{4}}=\dfrac{a+b+c}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}}=\dfrac{69}{\dfrac{23}{12}}=36\)
Do đó: a=18; b=24; c=27
Đúng 0
Bình luận (0)
Chia số 69 thành ba phần tỉ lệ với các số \(\dfrac{1}{2};\dfrac{2}{3}\) và \(\dfrac{3}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{2}}=\dfrac{b}{\dfrac{2}{3}}=\dfrac{c}{\dfrac{3}{4}}=\dfrac{a+b+c}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}}=\dfrac{69}{\dfrac{23}{12}}=36\)
Do đó: a=18; b=24; c=27
Đúng 0
Bình luận (0)
1 tìm các số hữu tỉ x,y thỏa mãn 3x2y và x+y-152 tìm các số hữu tỉ x,y biết rằng a) x+y-z20 và dfrac{x}{4}dfrac{y}{3}dfrac{z}{5}b)dfrac{x}{11}dfrac{y}{12};dfrac{y}{3}dfrac{z}{7} và 2x-y+z1523) chia số 552 thành ba phần tỉ lệ nghịch 3;4;5 tính giá trị từng phần?chia số 315 thành 3 phần tỉ lệ nghịch với 3:4:6. tính giá trị mỗi phần?4 cho tỉ lệ thức dfrac{a}{b}dfrac{c}{d} chứng minh rằnga)dfrac{a+b}{a-b}dfrac{c+d}{c-d}b)dfrac{5a+2c}{5a+2d}dfrac{a-4c}{b-4d}cdfrac{ab}{cd}dfrac{left(a+bright)^2}{left(...
Đọc tiếp
1 tìm các số hữu tỉ x,y thỏa mãn 3x=2y và x+y=-15
2 tìm các số hữu tỉ x,y biết rằng
a) x+y-z=20 và \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}\)
b)\(\dfrac{x}{11}=\dfrac{y}{12};\dfrac{y}{3}=\dfrac{z}{7}\) và 2x-y+z=152
3) chia số 552 thành ba phần tỉ lệ nghịch 3;4;5 tính giá trị từng phần?
chia số 315 thành 3 phần tỉ lệ nghịch với 3:4:6. tính giá trị mỗi phần?
4 cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) chứng minh rằng
a)\(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b)\(\dfrac{5a+2c}{5a+2d}=\dfrac{a-4c}{b-4d}\)
c\(\dfrac{ab}{cd}=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\)
Các bạn giúp mình với nhé mình dang cần gấp.mình xin cảm ơn
Bài 1:
Ta có: \(3x=2y\)
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
mà x+y=-15
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{-15}{5}=-3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-3\\\dfrac{y}{3}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-9\end{matrix}\right.\)
Vậy: (x,y)=(-6;-9)
Đúng 1
Bình luận (0)
Bài 2:
a) Ta có: \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}\)
mà x+y-z=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y-z}{4+3-5}=\dfrac{20}{2}=10\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{4}=10\\\dfrac{y}{3}=10\\\dfrac{z}{5}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=40\\y=30\\z=50\end{matrix}\right.\)
Vậy: (x,y,z)=(40;30;50)
Đúng 1
Bình luận (0)
Bài 2:
b) Ta có: \(\dfrac{y}{3}=\dfrac{z}{7}\)
nên \(\dfrac{y}{12}=\dfrac{z}{28}\)
mà \(\dfrac{x}{11}=\dfrac{y}{12}\)
nên \(\dfrac{x}{11}=\dfrac{y}{12}=\dfrac{z}{28}\)
hay \(\dfrac{2x}{22}=\dfrac{y}{12}=\dfrac{z}{28}\)
mà 2x-y+z=152
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x}{22}=\dfrac{y}{12}=\dfrac{z}{28}=\dfrac{2x-y+z}{22-12+28}=\dfrac{152}{38}=4\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{11}=4\\\dfrac{y}{12}=4\\\dfrac{z}{28}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=44\\y=48\\z=112\end{matrix}\right.\)
Vậy: (x,y,z)=(44;48;112)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
hãy chia số 786 thành những phần tỉ lệ nghịch với các số 0,2 , \(3\dfrac{1}{3}\) , \(\dfrac{4}{5}\)
Gọi ba phần cần tìm lần lượt là a,b,c
Theo đề, ta có: \(\dfrac{1}{5}a=\dfrac{10}{3}b=\dfrac{4}{5}c\)
=>\(\dfrac{a}{5}=\dfrac{b}{\dfrac{5}{4}}=\dfrac{c}{\dfrac{3}{10}}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{5}=\dfrac{b}{\dfrac{5}{4}}=\dfrac{c}{\dfrac{3}{10}}=\dfrac{a+b+c}{5+\dfrac{5}{4}+\dfrac{3}{10}}=\dfrac{786}{\dfrac{131}{20}}=120\)
=>a=600; b=150; c=36
Đúng 2
Bình luận (0)
Số M được chia thành 3 số tỉ lệ với \(\dfrac{1}{2}\);\(\dfrac{2}{3}\) ;\(\dfrac{3}{4}\) tìm số M biết tổng bình phương của 3 số đó bằng 724
Gọi ba số cần tìm là a,b,c
Đặt \(\dfrac{a}{2}=\dfrac{b}{\dfrac{3}{2}}=\dfrac{c}{\dfrac{4}{3}}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k\\b=\dfrac{3}{2}k\\c=\dfrac{4}{3}k\end{matrix}\right.\)
Ta có: \(a^2+b^2+c^2=724\)
\(\Leftrightarrow4k^2+\dfrac{9}{4}k^2+\dfrac{16}{9}k^2=724\)
\(\Leftrightarrow k^2=\dfrac{26064}{289}\)
Trường hợp 1: \(k=\dfrac{12\sqrt{181}}{17}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=\dfrac{24\sqrt{181}}{17}\\b=\dfrac{3}{2}k=\dfrac{18\sqrt{181}}{17}\\c=\dfrac{4}{3}k=\dfrac{16\sqrt{181}}{17}\end{matrix}\right.\)
Trường hợp 2: \(k=\dfrac{-12\sqrt{181}}{17}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2k=\dfrac{-24\sqrt{181}}{17}\\b=\dfrac{3}{2}k=\dfrac{-18\sqrt{181}}{17}\\c=\dfrac{4}{3}k=\dfrac{-16\sqrt{181}}{17}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
chia số 552 thành 3 phần tỉ lệ thuận với 1/2, 2/3, 3/4
chia số 552 thành 3 phần. biết tỉ lệ thuận với 1 phần 2 / 2 phần 3 / 3 phần 4
Số A được chia thành 3 số tỉ lệ theo \(\dfrac{2}{3}\)\(\dfrac{3}{4}\)\(\dfrac{1}{6}\)Biết rằng tổng bình phương của 3 số đó bàng 24309. Tìm số A
Đáng lẽ nó phải có dấu chia ở giữa mấy phân số kia chứ =')?
Đúng 1
Bình luận (1)