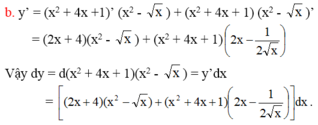Tìm TXD và TGT của các hàm số sau:
x2 +4x+3
Những câu hỏi liên quan
Tìm TXD và TGT của hàm số
1. y=\(\dfrac{-x+5}{2x+3}\)
2. y=\(\dfrac{3x+2}{2x-1}\)
1: ĐKXĐ: \(x\ne-\dfrac{3}{2}\)
2: ĐKXĐ: \(x\ne\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Tìm tập xác định của các hàm số sau: y = x 2 - 4 x + 3 - 2
Hàm số xác định khi x 2 − 4x + 3 ≠ 0 hay x ≠ 1; x ≠ 3.
Vậy tập xác định của hàm số đã cho là R \ {1;3}.
Đúng 0
Bình luận (0)
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau: y = 4 x − x 2
Tìm vi phân của các hàm số sau:
y
x
2
+
4
x
+
1
x
2
-
x
Đọc tiếp
Tìm vi phân của các hàm số sau: y = x 2 + 4 x + 1 x 2 - x
y=\(\sqrt{2-\dfrac{\sqrt{3}}{sinx}}\)tìm TXD của hàm số
ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\Rightarrow x\ne k\pi\\2-\dfrac{\sqrt{3}}{sinx}\ge0\left(1\right)\end{matrix}\right.\)
Xét (1):
\(\Leftrightarrow\dfrac{2sinx-\sqrt{3}}{sinx}\ge0\Leftrightarrow\left[{}\begin{matrix}sinx\ge\dfrac{\sqrt{3}}{2}\\sinx< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}+k2\pi\le x\le\dfrac{2\pi}{3}+k2\pi\\-\pi+k2\pi< x< k2\pi\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}\dfrac{\pi}{3}+k2\pi\le x\le\dfrac{2\pi}{3}+k2\pi\\-\pi+k2\pi< x< k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm tất cả các đường tiệm cận của đồ thị hàm số
y
x
-
x
2
-
4
x
2
-
4
x
+
3
là A. y 1 và x 3 B. y 0, y 1 và x 3 C. y 0 và x 3, x 1 D. y 0 và...
Đọc tiếp
Tìm tất cả các đường tiệm cận của đồ thị hàm số y = x - x 2 - 4 x 2 - 4 x + 3 là
A. y = 1 và x = 3
B. y = 0, y = 1 và x = 3
C. y = 0 và x = 3, x = 1
D. y = 0 và x = 3
SGK Chân trời sáng tạo trang 16
12 tháng 9 2023 lúc 23:11
Tìm các hàm số bậc nhất trong các hàm số sau đây và chỉ ra các hệ số \(a,b\) của các hàm số đó:
\(y = 4x - 7\);\(y = {x^2}\);\(y = - 6x - 4\);\(y = 4x\);\(y = \dfrac{3}{x}\);\(s = 5v + 8\);\(m = 30n - 25\).
- Hàm số\(y = 4x - 7\) là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 4;b = - 7\).
- Hàm số \(y = {x^2}\) không là hàm số bậc nhất vì hàm số không có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
- Hàm số \(y = - 6x - 4\)là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = - 6;b = - 4\).
- Hàm số \(y = 4x\)là hàm số bậc nhất vì hàm số có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 4;b = 0\).
- Hàm số \(y = \dfrac{3}{x}\) không là hàm số bậc nhất vì hàm số không có dạng \(y = ax + b\)với \(a,b\) là các số cho trước và \(a \ne 0\).
- Hàm số \(s = 5v + 8\) là hàm số bậc nhất vì hàm số có dạng \(s = av + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 5;b = 8\).
- Hàm số \(m = 30n - 25\) là hàm số bậc nhất vì hàm số có dạng \(m = an + b\)với \(a,b\) là các số cho trước và \(a \ne 0\). Hệ số \(a = 30;b = - 25\).
Đúng 0
Bình luận (0)
Cho các hình vẽ sau: a) Hình vẽ nào là đồ thị của hàm số
y
x
2
-
4
x
+
3
? A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Đọc tiếp
Cho các hình vẽ sau:
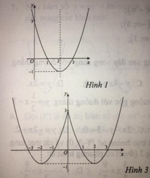
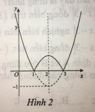
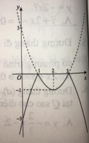
a) Hình vẽ nào là đồ thị của hàm số y = x 2 - 4 x + 3 ?
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Đồ thị của hàm số y = x2 – 4x + 3 là đường cong parabol nên chọn A.
Đúng 0
Bình luận (0)
Cho các hình vẽ sau: c) Hình vẽ nào là đồ thị của hàm số
y
x
2
-
4
x
+
3
? A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Đọc tiếp
Cho các hình vẽ sau:
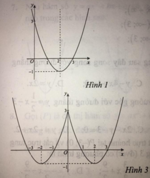
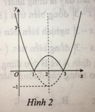
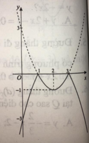
c) Hình vẽ nào là đồ thị của hàm số y = x 2 - 4 x + 3 ?
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Ta có: y = x 2 - 4 x + 3 = x 2 - 4 x + 3 k h i x 2 - 4 x + 3 ≥ 0 - x 2 - 4 x + 3 k h i x 2 - 4 x + 3 < 0
Cách vẽ đồ thị y = x 2 - 4 x + 3
+ Vẽ đồ thị hàm số y = x2 – 4x + 3 (C).
+ Giữ nguyên phần đồ thị (C) phía trên trục hoành
Lấy đối xứng phần dưới trục hoành qua trục hoành; xóa phần đồ thị (C) dưới trục hoành.
Khi đó, ta được đồ thị hàm số y = x 2 - 4 x + 3 .
Chọn B
Đúng 0
Bình luận (0)