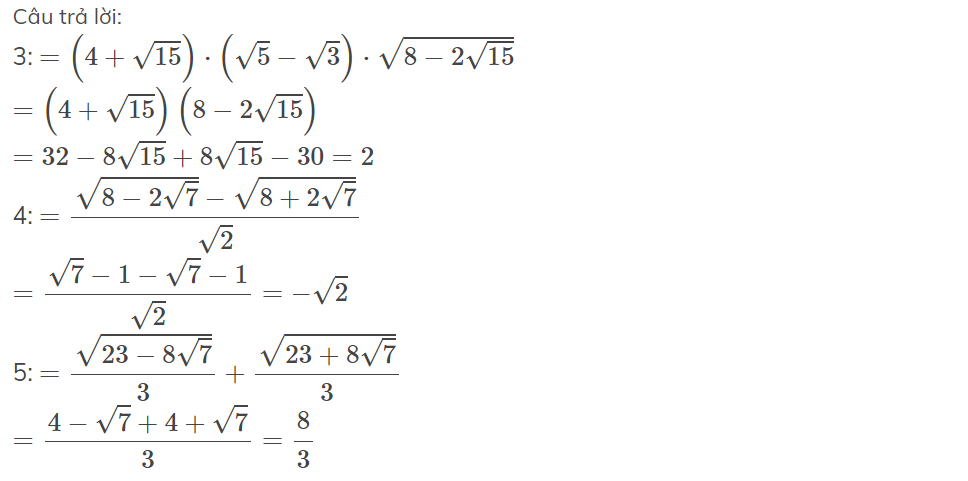\(T=\frac{\sqrt{2}.\left(4+\sqrt{7}\right)}{\sqrt{2}.\left(2\sqrt{2}+\sqrt{4+\sqrt{7}}\right)}+\frac{\sqrt{2}.\left(4-\sqrt{7}\right)}{\sqrt{2}.\left(2\sqrt{2}-\sqrt{4-\sqrt{7}}\right)}\)

\(T=\frac{4\sqrt{2}+\sqrt{14}}{4+\sqrt{8+2\sqrt{7}}}+\frac{4\sqrt{2}-\sqrt{14}}{4-\sqrt{8-2\sqrt{7}}}\)

\(T=\frac{4\sqrt{2}+\sqrt{14}}{4+\sqrt{7+2\sqrt{7}+1}}+\frac{4\sqrt{2}-\sqrt{14}}{4-\sqrt{7-2\sqrt{7}+1}}\)

\(T=\frac{4\sqrt{2}+\sqrt{14}}{4+\left(\sqrt{7}+1\right)^2}+\frac{4\sqrt{2}-\sqrt{14}}{4-\left(\sqrt{7}-1\right)^2}\)\(T=\frac{4\sqrt{2}+\sqrt{14}}{4+|\sqrt{7}+1|}+\frac{4\sqrt{2}-\sqrt{14}}{4-|\sqrt{7}-1|}\)

\(T=\frac{4\sqrt{2}+\sqrt{14}}{4+\sqrt{7}+1}+\frac{4\sqrt{2}-\sqrt{14}}{4-\sqrt{7}+1}\)

\(T=\frac{4\sqrt{2}+\sqrt{14}}{5+\sqrt{7}}+\frac{4\sqrt{2}-\sqrt{14}}{5-\sqrt{7}}\)

\(T=\frac{\left(4\sqrt{2}+\sqrt{14}\right).\left(5-\sqrt{7}\right)}{\left(5+\sqrt{7}\right).\left(5-\sqrt{7}\right)}+\frac{\left(4\sqrt{2}-\sqrt{14}\right).\left(5+\sqrt{7}\right)}{\left(5+\sqrt{7}\right).\left(5-\sqrt{7}\right)}\)

\(T=\frac{20\sqrt{2}-\sqrt{98}}{9}\)

\(T=\frac{13\sqrt{2}}{9}\)

B = \(\frac{4+\sqrt{7}}{3\sqrt{2}+\sqrt{4+\sqrt{7}}}+\frac{4-\sqrt{7}}{3\sqrt{2}-\sqrt{4-\sqrt{7}}}\)

=>  \(\frac{2}{\sqrt{2}}B=\frac{8+2\sqrt{7}}{6+\sqrt{8+2\sqrt{7}}}+\frac{8-2\sqrt{7}}{6-\sqrt{8-2\sqrt{7}}}\)

=> \(\frac{2}{\sqrt{2}}B=\frac{\left(\sqrt{7}+1\right)^2}{6+\sqrt{7}+1}+\frac{\left(\sqrt{7}-1\right)^2}{6-\sqrt{7}+1}\)

=> \(\frac{2}{\sqrt{2}}B=\frac{\left(\sqrt{7}+1\right)^2}{\sqrt{7}\left(\sqrt{7}+1\right)}+\frac{\left(\sqrt{7}-1\right)^2}{\sqrt{7}\left(\sqrt{7}-1\right)}\)

=> \(\frac{2}{\sqrt{2}}B=\frac{\sqrt{7}+1}{\sqrt{7}}+\frac{\sqrt{7}-1}{\sqrt{7}}=\frac{2\sqrt{7}}{\sqrt{7}}=2\)

=> B = \(\sqrt{2}\)

\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}-\sqrt{2}\)

\(=\dfrac{\sqrt{8-2\sqrt{7}}}{\sqrt{2}}-\dfrac{\sqrt{8+2\sqrt{7}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{7-2\sqrt{7}.1+1}}{\sqrt{2}}-\dfrac{\sqrt{7+2\sqrt{7}.1+1}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{7}-1-\sqrt{7}-1}{\sqrt{2}}\)

\(=-\dfrac{2}{\sqrt{2}}\)

\(=-\sqrt{2}\)

3: \(=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)

\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)

\(=32-8\sqrt{15}+8\sqrt{15}-30=2\)

4: \(=\dfrac{\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{7}-1-\sqrt{7}-1}{\sqrt{2}}=-\sqrt{2}\)

5: \(=\dfrac{\sqrt{23-8\sqrt{7}}}{3}+\dfrac{\sqrt{23+8\sqrt{7}}}{3}\)

\(=\dfrac{4-\sqrt{7}+4+\sqrt{7}}{3}=\dfrac{8}{3}\)

a) \(\sqrt{2}\left(\sqrt{4+\sqrt{7}}+\sqrt{4-\sqrt{7}}\right)\)

\(=\sqrt{2\cdot\left(4+\sqrt{7}\right)}+\sqrt{2\cdot\left(4-\sqrt{7}\right)}\)

\(=\sqrt{8+2\sqrt{7}}+\sqrt{8-2\sqrt{7}}\)

\(=\sqrt{\left(\sqrt{7}\right)^2+2\cdot\sqrt{7}\cdot1+1^2}+\sqrt{\left(\sqrt{7}\right)^2-2\cdot\sqrt{7}\cdot1+1^2}\)

\(=\sqrt{\left(\sqrt{7}+1\right)^2}+\sqrt{\left(\sqrt{7}-1\right)^2}\)

\(=\left|\sqrt{7}+1\right|+\left|\sqrt{7}-1\right|\)

\(=\sqrt{7}+1+\sqrt{7}-1\)

\(=2\sqrt{7}\)

b) \(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)

\(=\dfrac{\sqrt{2}\cdot\left(\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\right)}{\sqrt{2}}\)

\(=\dfrac{\sqrt{2\cdot\left(2-\sqrt{3}\right)}-\sqrt{2\cdot\left(2+\sqrt{3}\right)}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot1+1^2}-\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot1+1^2}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}}{\sqrt{2}}\)

\(=\dfrac{\left|\sqrt{3}-1\right|-\left|\sqrt{3}+1\right|}{\sqrt{2}}\)

\(=\dfrac{\sqrt{3}-1-\sqrt{3}-1}{ }\)

\(=-\dfrac{2}{\sqrt{2}}\)

\(=-\sqrt{2}\)

g: \(=\left|\sqrt{6}-1\right|=\sqrt{6}-1\)

h: \(=\left|2\sqrt{3}-1\right|=2\sqrt{3}-1\)

l: \(=\left|2-\sqrt{3}\right|-2=2-\sqrt{3}-2=-\sqrt{3}\)

j: \(=\left|3-\sqrt{6}\right|+\left|2\sqrt{6}-3\right|\)

\(=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)

a: =2-căn 3-2-căn 3

=-2căn 3

b: \(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8+2\sqrt{7}}-\sqrt{8-2\sqrt{7}}\right)\)

\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{7}+1-\sqrt{7}+1\right)=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)

c: \(A=\sqrt{4-\sqrt{10-2\sqrt{5}}}-\sqrt{4+\sqrt{10-2\sqrt{5}}}\)

=>\(A^2=4-\sqrt{10-2\sqrt{5}}+4+\sqrt{10-2\sqrt{5}}+2\cdot\sqrt{16-10+2\sqrt{5}}\)

\(\Leftrightarrow A^2=8+2\left(\sqrt{5}+1\right)=10+2\sqrt{5}\)

=>\(A=\sqrt{10+2\sqrt{5}}\)

Bài 2:

a) \(2\sqrt{125}+\dfrac{3}{2}\sqrt{80}-\sqrt{180}-\dfrac{2}{7}\sqrt{245}\)

\(=2\sqrt{5^2\cdot5}+\dfrac{3}{2}\sqrt{4^2\cdot5}-\sqrt{6^2\cdot5}-\dfrac{2}{7}\sqrt{7^2\cdot5}\)

\(=10\sqrt{5}+\dfrac{3\cdot4}{2}\sqrt{5}-6\sqrt{5}-\dfrac{2\cdot7}{7}\sqrt{5}\)

\(=10\sqrt{5}+6\sqrt{6}-6\sqrt{5}-2\sqrt{5}\)

\(=8\sqrt{5}\)

b) \(\sqrt{11-4\sqrt{7}}-\sqrt{16+6\sqrt{7}}\)

\(=\sqrt{\left(\sqrt{7}\right)^2-2\cdot2\cdot\sqrt{7}+2^2}-\sqrt{\left(\sqrt{7}\right)^2+2\cdot3\cdot\sqrt{7}+3^2}\)

\(=\sqrt{\left(\sqrt{7}-2\right)^2}-\sqrt{\left(\sqrt{7}+3\right)^2}\)

\(=\sqrt{7}-2-\sqrt{7}-3\)

\(=-5\)

\(2a,\\ 2\sqrt{125}+\dfrac{3}{2}.\sqrt{80}-\sqrt{180}-\dfrac{2}{7}\sqrt{245}\\ =2\sqrt{5^2.5}+\dfrac{3}{2}.\sqrt{4^2.5}-\sqrt{6^2.5}-\dfrac{2}{7}.\sqrt{7^2.5}\\ =2.5.\sqrt{5}+\dfrac{3}{2}.4.\sqrt{5}-6\sqrt{5}-\dfrac{2}{7}.7\sqrt{5}\\ =10\sqrt{5}+6\sqrt{5}-6\sqrt{5}-2\sqrt{5}=8\sqrt{5}\)

3: 

a: =>|x-1|=4

=>x-1=4 hoặc x-1=-4

=>x=-3 hoặc x=5

b: =>|6x-5|=4

=>6x-5=4 hoặc 6x-5=-4

=>6x=1 hoặc 6x=9

=>x=1/6 hoặc x=3/2