1.Một xe chuyển động thẳng nhanh dần đều đi trên hai đoạn đường liên tiếp bằng 5s và

Những câu hỏi liên quan
Một xe chuyển động thẳng nhanh dần đều đi trên hai đoạn đường liên tiếp bằng nhau 100m, lần lượt trong 5s và 3s. Tính gia tốc của xe. A.
3
10
m
/
s
2
B.
8
3
m
/
s
2
C....
Đọc tiếp
Một xe chuyển động thẳng nhanh dần đều đi trên hai đoạn đường liên tiếp bằng nhau 100m, lần lượt trong 5s và 3s. Tính gia tốc của xe.
A. 3 10 m / s 2
B. 8 3 m / s 2
C. 3 8 m / s 2
D. 10 3 m / s 2
Một xe chuyển động thẳng nhanh dần đều đi trên hai đoạn đường liên tiếp bằng nhau 100m, lần lượt trong 5s và 3s. Tính gia tốc của xe

Trong một 100m tiếp theo chuyển động hết 3s tức là 200m xe chuyển động hết 8s :
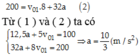
Đúng 0
Bình luận (0)
Một xe chuyển động thẳng nhanh dần đều đi trên hai đoạn đường liên tiếp bằng nhau 100m, lần lượt trong 5s và 3s. Tính gia tốc của xe.
Giải:
Áp dụng công thức s = v 0 t + 1 2 a t 2
Trong 100m đầu tiện : 100 = v 01 .5 + 12 , 5 a 1
Trong một 100m tiếp theo chuyển động hết 3s tức là 200m xe chuyển động hết 8s : 200 = v 01 .8 + 32 a 2
Từ ( 1 ) và ( 2 ) ta có 12 , 5 a + 5 v 01 = 100 32 a + 8 v 01 = 200 ⇒ a = 10 3 ( m / s 2 )
Đúng 0
Bình luận (0)
Một xe chuyển động nhanh dần đều đi trên hai đoạn đường liên tiếp bằng nhau 100 m lần lượt trong 5s và 3s. Gia tốc của xe là
Ta có:
\(s=v_0t+\dfrac{1}{2}at^2\)
100m đầu: \(5v_0+\dfrac{1}{2}\cdot5^2\cdot a=5v_0+12,5a=100\) (1)
200m sau chuyển động trong 8s: \(8v_0+\dfrac{1}{2}\cdot8^2\cdot a=8v_0+32a=200\) (2)
Từ (1) và (2) ta có hệ:
\(\left\{{}\begin{matrix}5v_0+12,5a=100\\8v_0+32a=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v_0=\dfrac{35}{3}\left(m/s\right)\\a=\dfrac{10}{3}\left(m/s^2\right)\end{matrix}\right.\)
Vậy: ...
Đúng 2
Bình luận (0)
một xe chuyển động nhanh dần đều đi trên 2 đoạn đường liên tiếp bằng nhau 100m lần lượt trong 5s và 3.5s tìm gia tốc xe
Bạn tham khảo: https://hoc24.vn/cau-hoi/mot-xe-chuyen-dong-nhanh-dan-deu-di-tren-2-doan-duong-lien-tiep-bang-nhau-100m-lan-luot-trong-5s-va-trong-35s-tinh-gia-toc-cua-xe.164124867230
Đúng 0
Bình luận (0)
Một xe chuyển động thẳng nhanh dần đều trên hai đoạn đường liên tiếp bằng nhau
100 m, lần lượt trong 10 s và 5 s. Tính gia tốc của xe?
Giúp mình bài này với ạ
Trên đoạn đường 100m đi với thời gian 10s:
\(S_1=v_0t+\dfrac{1}{2}at^2=10v_0+\dfrac{1}{2}\cdot a\cdot10^2=100\left(1\right)\)
Trên đoạn đường 200m đi với thời gian 15s:
\(S_2=v_0t+\dfrac{1}{2}at^2=15v_0+\dfrac{1}{2}\cdot a\cdot15^2=200\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow v_0=\dfrac{10}{3}\)m/s và \(a=\dfrac{4}{3}\)m/s2
Đúng 2
Bình luận (0)
Một xe chuyển động nhanh dần đều đi trên 2 đoạn đường liên tiếp bằng nhau bằng S0 lần lượt hết 5s và 3,5s. Tính gia tốc
1,gọi gia tốc là: a
=>he: S1= Vt +0,5at^2=100
S2= (V+at)t +0,5at^2=100
<=> he: S1=5V +25A/2=100
S2=7V/2 +99a/4= 100
<=> V=245/16(m/s)
a=15/8 (m/s^2)
4,tau di: S=5t +0,15t^2
oto: S= 0,25t^2
Gap nhau: 5t +0,15t^2= 0,25t^2
<=> t=50s
Đúng 0
Bình luận (0)
Câu 2 (1 điểm) Một chất điểm chuyển động thẳng trên ba đoạn đường liên tiếp AB, BC và CD. Trên đoạn AB dài 36m chất điểm chuyển động nhanh dần đều không vận tốc đầu trong thời gian 6s. Tiếp theo trên đoạn BC chất điểm chuyển động thẳng đều trong thời gian 20s. Trên đoạn CD dài 9m chất điểm chuyển động chậm dần đều cho đến khi dừng lại tại D. Tính gia tốc chuyển động trên mỗi đoạn đường và vận tốc trung bình trên cả đoạn đường đó.
Đọc tiếp
Câu 2 (1 điểm) Một chất điểm chuyển động thẳng trên ba đoạn đường liên tiếp AB, BC và CD. Trên đoạn AB dài 36m chất điểm chuyển động nhanh dần đều không vận tốc đầu trong thời gian 6s. Tiếp theo trên đoạn BC chất điểm chuyển động thẳng đều trong thời gian 20s. Trên đoạn CD dài 9m chất điểm chuyển động chậm dần đều cho đến khi dừng lại tại D. Tính gia tốc chuyển động trên mỗi đoạn đường và vận tốc trung bình trên cả đoạn đường đó.
Một xe chuyển động nhanh dần đều đi trên 2 đoạn đường liên tiếp bằng nhau 100m, lần lượt trong 5s và trong 3,5s. Tính gia tốc của xe
gọi v0 là vận tốc ban đầu, a là gia tốc
100m đầu tiên : s1=v0.t1+\(\dfrac{1}{2}\)at12=5v0+12,5a=100 (1)
Cả hai quãng đường : s2=v0.(t1+t2)+\(\dfrac{1}{2}\)a(t1+t2)2=8,5v0+36,125a=200 (2)
giải hê phương trình (1) và (2) ta được v0=14,958(m/s) a=2,017(m/s2)
Đúng 1
Bình luận (3)
Trên đường thẳng, ô tô chuyển động nhanh dần đều trên hai đoạn đường liên tiếp bằng nhau và bằng 150 m, lần lượt trong 6 s và 3 s. Gia tốc của ô tô gần giá trị nào nhất sau đây? A.
7
,
2
m
/
s
2
B.
2
,
1
m
/
s
2
C.
5
,
6
m
/...
Đọc tiếp
Trên đường thẳng, ô tô chuyển động nhanh dần đều trên hai đoạn đường liên tiếp bằng nhau và bằng 150 m, lần lượt trong 6 s và 3 s. Gia tốc của ô tô gần giá trị nào nhất sau đây?
A. 7 , 2 m / s 2
B. 2 , 1 m / s 2
C. 5 , 6 m / s 2
D. 4 , 3 m / s 2




















