Cho hình vẽ , hãy chứng tỏ Ax//By//Cz
A x B y C z 120 độ 80 độ 160 độ 120 độ
Đọc tiếp
Cho hình vẽ , hãy chứng tỏ Ax//By//Cz
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Những câu hỏi liên quan
B1 cho hình vẽ có Ax//By//Cz.Tính góc ACB.Biết góc xAC=30 độ , góc zCB=100 độ
B2 cho hình vẽ có góc ACB=110 độ và Ax//By//Cz.Tính góc B. Biết góc xAC=30 độ
B3 cho hình vẽ chứng tỏ
a>By//Cz
b>Ax//By
biết gócxAz=60 độ,góc Z1=120 độ,góc Z2=140 độ,góc zBy=40 độ
Bài 13: Cho hình vẽ. Chứng minh: Ax//By//Cz.
Bài 14: Cho hình vẽ. Biết mAx=60 độ; mBy= 120 độ, BCz=150 độ.Chứng minh: Ax//By//Cz. Giúpp mình với ạ. Mình đang cần gấpp.
Helpp
*Kẻ By’ là tia đối của tia By => ABy kề bù với ABy’
=> ABy + ABy’ = 180
=> 120 + ABy’ = 180
=> ABy’ = 60
Ta có mAx = 60 =ABy’ , mà mAx và ABy’ ở vị trí đồng vị => Ax // By (1)
*Ta có yBC + CBA + ABy = 360
=> yBC + 90 + 120 = 360
=> yBC = 150
Ta có BCz = 150 = yBC, mà 2 góc này ở vị trí so le trong => By // Cz (2)
Từ (1), (2) => đpcm
Đúng 0
Bình luận (0)
cho hình vẽ xÂB30 độ BCy120 độ Ax//Cy . Chứng tỏ CB vuông góc AB ? y C B A x
Đọc tiếp
cho hình vẽ xÂB=30 độ BCy=120 độ Ax//Cy . Chứng tỏ CB vuông góc AB ?
A x O B y 35độ 85 độ z 120 độ cho hình vẽ chứng tỏ Ax song song với By giúp mk với nha chiều mk đi học rồi<3<3<3
Cho Ax song song By. Tính ACB
m A x C z n B y 145 độ 120 độ 1 2
Đọc tiếp
Cho Ax song song By. Tính ACB
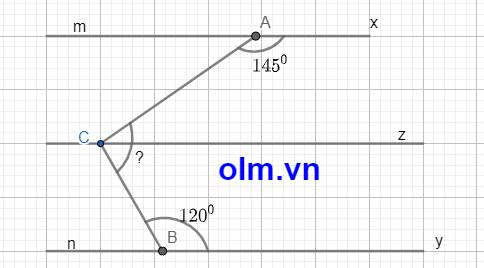
Ta có: \(\widehat{ACz}\) và \(\widehat{CAx}\) là hai góc trong cùng phía nên:
\(\widehat{ACz}\) + \(\widehat{CAx}\) = 1800 ⇒ \(\widehat{ACz}\) = 1800 - 1450 = 350
Mặt khác ta cũng có: \(\widehat{BCz}\) và \(\widehat{CBy}\) là hai góc trong cùng phía nên:
\(\widehat{BCz}\) + \(\widehat{CBy}\) = 1800 ⇒ \(\widehat{BCz}\) = 1800 - 1200 = 600
\(\widehat{ACB}\) = \(\widehat{ACz}\) + \(\widehat{BCz}\) = 350 + 600 = 950
Kết luận: \(\widehat{ACB}\) = 950
Đúng 1
Bình luận (0)
Cho góc xao=aob=120 độ, oby= 60 độ. Ot là tia pgiac của Boa. Chứng tỏ by//ot,ot//ax. Vẽ hô mình. Gợi ý cách vẽ chỉ giống chữ z xíu. Nhanh mình tick
cho hình vẽ biết góc xAB = 110 độ, ABC = 120 độ, zCB = 130 độ , vBC = 130 độ. Chứng minh Ax // Bv // Cz
help me ~
30 tháng 8 2023 lúc 9:03
Cho hình vẽ:
45* 135* 75* 30* A x B C y z
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
Đọc tiếp
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
Đúng 0
Bình luận (0)
Cho Ax//By//Cz
A=120 độ, B=140 độ
Tính ACB
\(\cdot\text{Do Ax//Cz}\)
\(\Rightarrow\widehat{xAC}+\widehat{ACz}=180^o\left(\text{trong cùng phía}\right)\left(1\right)\)
\(\text{Thay }\widehat{xAC}=120^o\text{ vào }\left(1\right)\)
\(\Rightarrow120^o+\widehat{ACz}=180^o\)
\(\Rightarrow\widehat{ACz}=180^o-120^o\)
\(\Rightarrow\widehat{ACz}=60^o\)
\(\cdot\text{Do By//Cz}\)
\(\Rightarrow\widehat{yCB}+\widehat{BCz}=180^o\left(\text{trong cùng phía}\right)\left(2\right)\)
\(\text{Thay }\widehat{yBC}=140^o\text{ vào }\left(2\right)\)
\(\Rightarrow140^o+\widehat{BCz}=180^o\)
\(\Rightarrow\widehat{BCz}=180^o-140^o\)
\(\Rightarrow\widehat{BCz}=40^o\)
\(\cdot\text{Lại có: }\widehat{ACz}+\widehat{BCz}=\widehat{ACB}\)
\(\text{Mà }\widehat{ACz}=60^o;\widehat{BCz}=40^o\)
\(\Rightarrow60^o+40^o=\widehat{ACB}\)
\(\Rightarrow\widehat{ACB}=100^o\)
\(\text{Vậy }\widehat{ACB}=100^o\)
\(\text{Tổng quát: Nếu }\widehat{A}+\widehat{B}+\widehat{C}=360^o\text{ thì ta luôn chứng minh được Ax//By/Cz}\)
\(\text{Và nếu Ax//By//Cz và biết 2 trong 3 góc thì ta luôn tìm ra được 1 góc còn lại. }\)
cho góc xao=aob=120 độ, oby= 60 độ. ot là tia pgiac của boa. chứng tỏ by//ot,ot//ax. Vẽ hộ mình nha