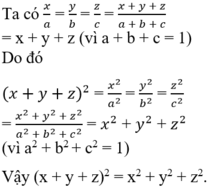CMR: Nếu x/a=y/b=z/c thì: (x2+y2+z2) (a2+b2+c2)=(ax+by+cz)2

Những câu hỏi liên quan
Bài 3 Chứng minh rằng với a, b, c, x, y, z (trong đó xyz 6 0) thỏa mãn (a2 + b2 + c2)(x2 + y2 + z2) (ax + by + cz)2 thì a/x b/y c/z.
Đọc tiếp
Bài 3 Chứng minh rằng với a, b, c, x, y, z (trong đó xyz 6= 0) thỏa mãn (a2 + b2 + c2)(x2 + y2 + z2) = (ax + by + cz)2
thì a/x =b/y =c/z.
Chứng minh rằng nếu: thì (x2 + y2 + z2) (a2 + b2 + c2) = (ax + by + cz)2
Chứng minh rằng nếu: thì (x2 + y2 + z2) (a2 + b2 + c2) = (ax + by + cz)2
3. Chứng minh rằng nếu: thì(x2 + y2 + z2) (a2 + b2 + c2) (ax + by + cz)2
Đọc tiếp
3. Chứng minh rằng nếu: thì
(x2 + y2 + z2) (a2 + b2 + c2) = (ax + by + cz)2
đặt x/a=y/b=z/c=k
=>x=a.k,
y=b.k
z=c.k
=>(a^2k^2+b^2k^2+c^2k^2)(a^2+b^2+c^2)=k^2.(a^2+b^2+c^2)^2(1)
(ax+by+cz)^2=(a.a.k+b.b.k+c.c.k)^2=(a^2.k+b^2.k+c^2.k)^2
=k^2(a^2+b^2+c^2)(2)
từ (1)(2)=> nếu x/a=y/b=z/c thì (x2 + y2 + z2) (a2 + b2 + c2) = (ax + by + cz)2
=>
Đúng 0
Bình luận (0)
Cho x, y , z khác 0. Cmr nếu a=x2-yz, b=y2-xz , c=z2-xy thì (ax+by+cz) chia hết cho (a+b+c)
help em gấp ạ
\(ax+by+cz\\ =x\left(x^2-yz\right)+y\left(y^2-xz\right)+z\left(z^2-xy\right)\\ =x^3+y^3+z^3-3xyz\\ =\left(x+y\right)^3-3xy\left(x+y\right)+z^3-3xyz\\ =\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2\right)-3xy\left(x+y+z\right)\\ =\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
Lại có \(a+b+c=x^2+y^2+z^2-xy-yz-xz\)
Vậy ta được đpcm
Đúng 3
Bình luận (0)
Cho a=x2 - yz; b= y2 - zx: c= z2 - xy.
a) Tính tổng ax+by+ cz và tổng a+b+c
b) CMR ax+by+ cz=(x +y + z)(a+b+c)
a: \(ax+by+cz\)
\(=x^3-xyz+y^3-xyz+z^3-xyz\)
\(=x^3+y^3+z^3-3xyz\)
Đúng 1
Bình luận (0)
Cho a=x2 - yz; b= y2 - zx: c= z2 - xy.
a) Tính tổng ax+by+ cz và tổng a+b+c
b) CMR ax+by+ cz=(x +y + z)(a+b+c
b: \(ax+by+cz\)
\(=x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3yxz\)
\(=\left(x+y+z\right)\left(x^2+y^2+2xy-xz-yz+z^2\right)-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
Đúng 0
Bình luận (0)
Cho a + b + c = a2 + b2 + c2 = 1 và x : y : z = a : b : c.
Chứng minh rằng: (x + y + z)2 = x2 + y2 + z2.
Cho a/x+b/y+C/z=2 và x/a+y/b+z/c=0 . Chứng minh A=x2/a2+y2/b2+z2/c2=1
Các số thực a,b,c,x,y,z thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
c
+
4
0
và
x
2
+
y
2
+
z
2
-
4
x
+
4
y
+
4...
Đọc tiếp
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
![]()
![]()
![]()
![]()





![Ckun []~( ̄▽ ̄)~*[]~( ̄▽...](https://hoc24.vn/images/avt/avt145702769_256by256.jpg)