Cho hình bình hành ABCD. Gọi N là trung điểm cạnh CD. Trên cạnh AC lấy điểm M sao cho AM = 2MC; Phân tích các vec tơ sau theo hai véc tơ ABvà AD
a. vecto ac
b) vecto AM
c) vecto an
Những câu hỏi liên quan
Cho hình bình hành ABCD .Trên cạnh AB lấy điểm M,trên cạnh CD lấy điểm N sao cho AM=CN
a.CM AMCN là hình bình hành
b.Gọi O là giao điểm của AC và BD.CM 3 điểm M,O,N thẳng hành\
c.Trên AD lấy điểm E,gọi F là giao điểm của EO với BC.CM EMFN là hình bình hành
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trên cạnh DC lấy điểm N sao cho AM=CN.
a/ Chứng minh AN//CM.
b/ Gọi O là giao điểm của AC và BD. Chứng minh O là trung điểm của MN.
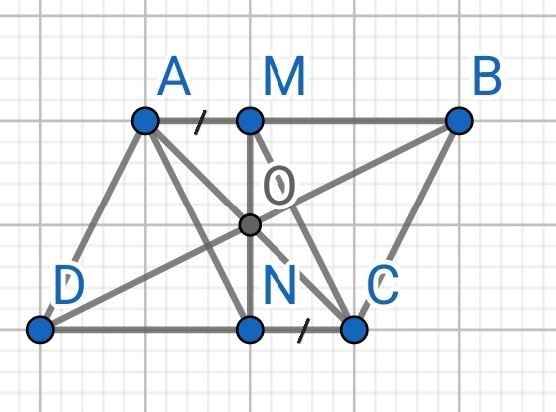a) Do ABCD là hình bình hành
AB // CD
⇒ AM // CN
Tứ giác AMCN có:
AM // CN (cmt)
AM = CN (gt)
⇒ AMCN là hình bình hành
⇒ AN // CM
b) Do ABCD là hình bình hành
O là giao điểm của AC và BD
⇒ O là trung điểm của AC
Lại có AMCN là hình bình hành
O là trung điểm của AC (cmt)
⇒ O là trung điểm của MN
Đúng 2
Bình luận (0)
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho AM=CN
a, CM AMCN là hình bình hành
b, CM DMBN là hình bình hành
a: Xét tứ giác AMCN có
AM//NC
AM=CN
=>AMCN là hình bình hành
b:
AM+MB=AB
CN+ND=CD
mà AM=CN và AB=CD
nên MB=ND
Xét tứ giác DMBN có
BM//DN
BM=DN
=>DMBN là hình bình hành
Đúng 1
Bình luận (0)
24 tháng 11 2023 lúc 19:31
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = CN.
a) Chứng minh AN//CM ;
b) Gọi O là giao điểm của AC và BD. Chứng minh O là trung điểm của MN.
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD, lấy trên các cạnh AB và CD điểm E và F sao cho AE = CF, trên cạnh AD và BC lấy điểm M và N sao cho AM = CN
a. Cm EMFN là hình bình hành
b. Gọi I là giao điểm AC và BD. C/m EF và MN cùng đi qua I
what the f''''ck
Sai rồi Em 😐😐😐
Cho hình bình hành ABCD. Trên cạnh AB và CD lấy M và N sao cho AM = CN.
a/ Chứng minh tứ giác AMCN là hình bình hành.
b/ Gọi O là giao điểm của AC và MN. Chứng minh O là trung điểm của BD.
Các bạn giúp mình với mình đang cần gấp ạ
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Đúng 0
Bình luận (0)
Hình bình hành ABCD . Trên cạnh AB và CD lấy M và N sao cho AM và CN .
a) Chứng minh rằng AMCN là hình bình hành
b) O là giao điểm của AC và MN chứng mình O là trung điểm của BC
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE=CF. Gọi O là giao điểm của AC và BD
1) Chứng minh tứ giác AECF là hình bình hành
2) Chứng minh O là trung điểm của EF
1) Vì ABCD là hình bình hành nên AB//CD hay AE//CF
Xét tứ giác AECF có AE//CF, AE=CF
=> AECF là hình bình hành
2) Vì AbCDlà hình bình hành nên O là trung điểm của AC (1)
Mà AECF là hình bình hành có 2 đường chéo AC và EF cắt nhau tại O (2)
Suy ra O là trung điểm của EF
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E và trên cạnh CD lấy điểm F sao cho AE = CF. Trên cạnh AD lấy điểm M và trên cạnh BC lấy điểm N sao cho AM = CN.
Tứ giác AECF là hình gì ? vì sao? Tứ giác MENF là hình gì? Vì sao?
Vì AE=CF và AE//CF (AB//CD do hbh ABCD) nên AECF là hbh
\(\left\{{}\begin{matrix}AE=CF\\AM=CN\\\widehat{A}=\widehat{C}\left(hbh.ABCD\right)\end{matrix}\right.\Rightarrow\Delta AME=\Delta CNF\left(c.g.c\right)\\ \Rightarrow ME=NF\left(4\right)\\ \left\{{}\begin{matrix}AE=CF\\AB=CD\end{matrix}\right.\Rightarrow AB-AE=CD-CF\Rightarrow BE=DF\left(1\right)\\ \left\{{}\begin{matrix}AM=CN\\AD=BC\end{matrix}\right.\Rightarrow AD-AM=CN-BC\Rightarrow DM=BN\left(2\right)\)
ABCD là hbh nên \(\widehat{B}=\widehat{D}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\Delta DMN=\Delta BFE\left(c.g.c\right)\\ \Rightarrow MN=EF\left(5\right)\)
(4)(5) suy ra MENF là hbh
Đúng 0
Bình luận (0)