Tìm k để giá trị nhỏ nhất của hàm số \(y=\dfrac{k\sin x+1}{\cos x+2}\) lớn hơn 1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=sin\dfrac{2x}{x^2+1}+cos\dfrac{x}{x^2+1}+1\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm k để giá trị nhỏ nhất của hàm số
y = f(x) = k sin x + 1 cos x + 2 lớn hơn -1?
A. k < 2
B. k < 2 3
C. k < 3
D. k < 2 2
Chọn D
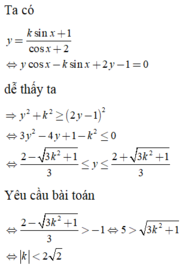
· Bổ trợ kiến thức: Để cho bài toán được dễ hiểu hơn các em có thể nghĩ hướng giải một cách đơn giản như sau, đầu tiên là các em dùng kiến thức về min, max của hàm số để tìm các GTLN và GTNN của hàm số ( kể cả có tham số hay không có tham số ), sau đó giải quyết min > –1 vậy là hoàn thành xong bài toán.
Bước khó khăn của bài toán trên là bước tìm min của 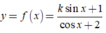
do gặp phải tham số k nhưng nếu dùng các kĩ thuật sơ cấp để xử lí và dễ tìm thấy được 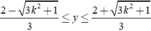 ,
,
khi đó ta chỉ cần tìm k sao cho min y > –1 vậy là ta chọn được đáp án đúng.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) y=f(x)=\(\dfrac{4}{\sqrt{5-2cos^2xsin^2x}}\)
b)y=f(x)=\(3sin^2x+5cos^2x-4cos2x-2\)
c)y=f(x)=\(sin^6x+cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số :
\(y=\sin^2x+4\sin x\cos x-3\cos^2x+1\)
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 2 là
A. m = - 1 2 ; M = 1
B. m = 1 ; M = 2
C. m = - 2 ; M = 1
D. m = - ; M = 2
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 2 là
![]()
![]()
![]()
![]()
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos x + 2 . sin x + 3 2 . cos x - sin x + 4 . Tính M,m
A. 4/11
B. 3/4
C. 1/2
D. 20/11
tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau
a)\(y=\left(3-sinx\right)^2+1\)
b)\(y=sin^4x+cos^4x\)
c)\(y=sin^6x+cos^6x\)
a)\(-1\le sinx\le1\)
\(\Leftrightarrow1\ge-sinx\ge-1\)
\(\Leftrightarrow4\ge3-sinx\ge2\) \(\Leftrightarrow16\ge\left(3-sinx\right)^2\ge4\)\(\Leftrightarrow17\ge\left(3-sinx\right)^2+1\ge5\)
\(\Leftrightarrow17\ge y\ge5\)
\(y_{min}=5\Leftrightarrow sinx=1\)\(\Leftrightarrow\)\(x=\dfrac{\pi}{2}+k2\pi\)\(\left(k\in Z\right)\)
\(y_{max}=17\Leftrightarrow\)\(sinx=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)\(\left(k\in Z\right)\)
b)\(y=\left(sin^2x+cos^2x\right)^2-2.sinx^2cos^2x\)\(=1-\dfrac{1}{2}.sin^22x\)
Có \(0\le sin^22x\le1\)\(\Leftrightarrow0\ge-\dfrac{1}{2}.sin^22x\ge-\dfrac{1}{2}\)
\(\Leftrightarrow1\ge1-\dfrac{1}{2}.sin^22x\ge\dfrac{1}{2}\)\(\Leftrightarrow1\ge y\ge\dfrac{1}{2}\)
\(y_{min}=\dfrac{1}{2}\Leftrightarrow sin^22x=1\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}sin2x=-1\\sin2x=1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
\(y_{max}=1\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\)\(\left(k\in Z\right)\)
c)\(y=\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=1-3sin^2x.cos^2x=1-\dfrac{3}{4}.sin^22x\)
Có \(0\le sin^22x\le1\)\(\Leftrightarrow0\ge-\dfrac{3}{4}.sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}.sin^22x\ge\dfrac{1}{4}\)\(\Leftrightarrow1\ge y\ge\dfrac{1}{4}\)
\(y_{min}=\dfrac{1}{4}\Leftrightarrow sin^22x=1\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(y_{max}=1\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\)\(\left(k\in Z\right)\)
Vậy...
a, Đặt \(t=sinx\left(t\in\left[-1;1\right]\right)\)
\(y=f\left(t\right)=\left(3-t\right)^2+1=t^2-6t+10\)
\(\Rightarrow min=min\left\{f\left(-1\right);f\left(1\right)\right\}=f\left(1\right)=5\)
\(\Rightarrow max=max\left\{f\left(-1\right);f\left(1\right)\right\}=f\left(-1\right)=17\)
b, \(y=sin^4x+cos^4x=1-2sin^2x.cos^2x=1-\dfrac{1}{2}sin^22x\)
Đặt \(t=sin2x\left(t\in\left[-1;1\right]\right)\)
\(y=f\left(t\right)=1-\dfrac{1}{2}t^2\)
\(\Rightarrow min=min\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=\dfrac{1}{2}\)
\(\Rightarrow max=max\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=1\)
c, \(y=sin^6x+cos^6x\)
\(=sin^4x+cos^4x-sin^2x.cos^2x\)
\(=1-3sin^2x.cos^2x\)
\(=1-\dfrac{3}{4}sin^22x\)
Đặt \(t=sin2x\left(t\in\left[-1;1\right]\right)\)
\(y=f\left(t\right)=1-\dfrac{3}{4}t^2\)
\(\Rightarrow min=min\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=\dfrac{1}{4}\)
\(\Rightarrow max=max\left\{f\left(-1\right);f\left(0\right);f\left(1\right)\right\}=1\)