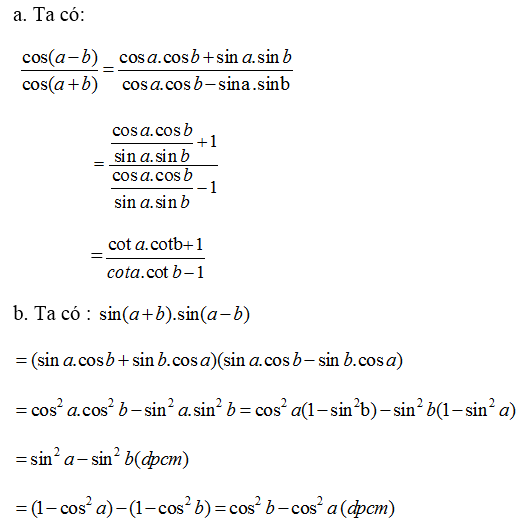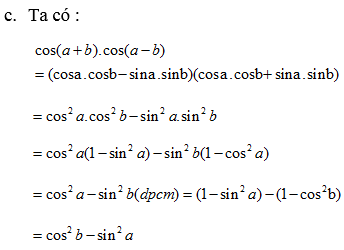a: sin a=2/3

=>cos^2a=1-(2/3)^2=5/9

=>\(cosa=\dfrac{\sqrt{5}}{3}\)

\(tana=\dfrac{2}{3}:\dfrac{\sqrt{5}}{3}=\dfrac{2}{\sqrt{5}}\)

\(cota=1:\dfrac{2}{\sqrt{5}}=\dfrac{\sqrt{5}}{2}\)

b: cos a=1/5

=>sin^2a=1-(1/5)^2=24/25

=>\(sina=\dfrac{2\sqrt{6}}{5}\)

\(tana=\dfrac{2\sqrt{6}}{5}:\dfrac{1}{5}=2\sqrt{6}\)

\(cota=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)

c: cot a=1/tana=1/2

\(1+tan^2a=\dfrac{1}{cos^2a}\)

=>1/cos^2a=1+4=5

=>cos^2a=1/5

=>cosa=1/căn 5

\(sina=\sqrt{1-cos^2a}=\dfrac{2}{\sqrt{5}}\)

1: 

a: sin a=căn 3/2

\(cosa=\sqrt{1-sin^2a}=\sqrt{1-\dfrac{3}{4}}=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}\)

\(tana=\dfrac{\sqrt{3}}{2}:\dfrac{1}{2}=\sqrt{3}\)

cot a=1/tan a=1/căn 3

b: \(tana=2\)

=>cot a=1/tan a=1/2

\(1+tan^2a=\dfrac{1}{cos^2a}\)

=>\(\dfrac{1}{cos^2a}=5\)

=>cos^2a=1/5

=>cosa=1/căn 5

\(sina=\sqrt{1-cos^2a}=\sqrt{\dfrac{4}{5}}=\dfrac{2}{\sqrt{5}}\)

c: \(cosa=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)

tan a=5/13:12/13=5/12

cot a=1:5/12=12/5

a, \(\left(1-sin^2x\right)cot^2x+1-cot^2x\)

\(=cot^2x-sin^2x.cot^2x+1-cot^2x\)

\(=1-sin^2x.\frac{\text{cos}^2x}{sin^2x}=1-\text{cos}^2x=sin^2x\)

b,\(\left(tanx+cotx\right)^2-\left(tanx-cotx\right)2\)

\(=tan^2x2.tanx.cotx+cot^2x-tan^2x+2tanx.cotx-cot^2x\)

\(=4tanxcotx=4\)

c,\(\left(xsina-y\text{cos}a\right)^2+\left(x\text{cos}a+ysina\right)^2\)

\(=x^2sin^2a=2xysina\text{cos}a+y^2\text{cos}^2a+2xysina\text{cos}a+y^2sin^2a\)

\(=x^2\left(sin^2a+\text{cos}^2a\right)+y^2\left(sin^2a+\text{cos}^2a\right)\)

\(=x^2+y^2\)

\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)

\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)

\(\Rightarrow P=4\)

\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)

\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)

\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)

1. Ta có \(1+\tan\alpha=\dfrac{1}{\cos^2\alpha}\Rightarrow\dfrac{1}{\cos^2\alpha}=1+\dfrac{1}{3}\Rightarrow\dfrac{1}{\cos^2\alpha}=\dfrac{4}{3}\Rightarrow\cos^2\alpha=\dfrac{3}{4}\Rightarrow\cos\alpha=\dfrac{\sqrt{3}}{2}\)

Mặt khác, \(tan\alpha=\dfrac{1}{3}=\dfrac{\sin\alpha}{\cos\alpha}\Rightarrow\sin\alpha=\dfrac{\cos a}{3}=\dfrac{\dfrac{\sqrt{3}}{2}}{3}=\dfrac{1}{2\sqrt{3}}\)

2. Ta có \(1+\cot^2\alpha=\dfrac{1}{\sin^2\alpha}\Rightarrow\dfrac{1}{\sin^2\alpha}=1+\dfrac{9}{16}\Rightarrow\dfrac{1}{\sin^2\alpha}=\dfrac{25}{16}\Rightarrow\dfrac{1}{\sin a}=\dfrac{5}{4}\Rightarrow\sin\alpha=\dfrac{4}{5}\)

Mặt khác, \(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}\Rightarrow\cos\alpha=\sin\alpha.\cot\alpha=\dfrac{3}{4}.\dfrac{4}{5}=\dfrac{3}{5}\)

Ta có: \(\sin^2\alpha+\cos^2\alpha=1\)

\(\Leftrightarrow\cos^2\alpha=1-\sin^2\alpha=1-\left(\frac{1}{5}\right)^2=\frac{24}{25}\)

\(\Leftrightarrow\cos\alpha=\frac{2\sqrt{6}}{5}\)

\(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\frac{1}{5}}{\frac{2\sqrt{6}}{5}}=\frac{\sqrt{6}}{12}\)

\(\tan\alpha.\cot\alpha=1\)

\(\Leftrightarrow\cot\alpha=\frac{1}{\tan\alpha}=\frac{1}{\frac{\sqrt{6}}{12}}=2\sqrt{6}\)

Chúc bạn hok tốt!!! nguyenthitonga