A B 40 C D 130 E F
Chứng tỏ rằng:
CD // EF
AB // CD
Đọc tiếp
Chứng tỏ rằng:
CD // EF
AB // CD
Những câu hỏi liên quan
Cho hình vẽ, chứng minh rằng AB//CD//EF A C B D F E 70 độ
Đọc tiếp
Cho hình vẽ, chứng minh rằng AB//CD//EF
cho hình thang ABCD có AB // CD góc C + D bằng 90 độ, CD > AB. gọi E, F theo thứ tự là trung điểm của các cạnh AB và CD. chứng minh rằng EF = CD - AD : 2
Câu hỏi của headsot96 - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo!
Đúng 0
Bình luận (0)
chứng tỏ AB//EF trong mỗi hình sauhình a A B C D E F 120 độ 60 độ 40 độ 140 độ hình b C D E F A B 30 độ 30 độ 40 độ 40 độ
Đọc tiếp
chứng tỏ AB//EF trong mỗi hình sau
hình a
hình b
hình a, ta thấy
\(\angle\left(A\right)+\angle\left(DCA\right)=120+60=180^0\)
mà 2 góc này ở vị trí trong cùng phía
\(=>AB//CD\left(1\right)\)
có \(\angle\left(DCE\right)+\angle\left(E\right)=40+140=180^O\)
mà 2 góc này ở vị trí trong cùng phía
\(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
hình b,
\(=\angle\left(BAD\right)=\angle\left(ADC\right)=30^0\)
mà 2 góc này ở vị trí so le trong \(=>AB//CD\left(1\right)\)
có \(\angle\left(CDE\right)=\angle\left(DEF\right)=40^o\)
mà 2 góc này ở vị trí so le trong \(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
Đúng 2
Bình luận (0)
Cho hình thang ABCD (AB//CD, AB CD) hai tia phân giác của
B
^
v
à
C
^
cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt AB, CD lần lượt ở E và F.a) Tìm các hình thang.b) Chứng minh rằng tam giác BEI cân ở E và tam giác IFC cân ở F.c) Chứng minh EF BE + CF
Đọc tiếp
Cho hình thang ABCD (AB//CD, AB < CD) hai tia phân giác của B ^ v à C ^ cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt AB, CD lần lượt ở E và F.
a) Tìm các hình thang.
b) Chứng minh rằng tam giác BEI cân ở E và tam giác IFC cân ở F.
c) Chứng minh EF = BE + CF
a) HS tự tìm
b) Sử dụng các cặp góc so le trong của hai đường thẳng song song và tính chất tia phân giác.
c) Suy ra từ b)
Đúng 0
Bình luận (0)
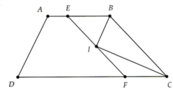
Cho hình thang ABCD (AB//CD) gọi E , F , K lần lượt là trung điểm của Ad , AC , BC a) Chứng minh EF//CD b) Chứng minh EK//CD c) Chứng minh ba điểm E,F,K thẳng hàng
Cho hình thang ABCD có đáy lớn CD . Qua A kẻ AK song song BC . Qua B kẻ BI song song AD ( K và I thuộc CD ). BI cắt AC tại F . AK cắt BD tại E . Chứng minh rằng :
a. EF song song AB
b. AB mũ 2 = CD . EF
ế, đây là toán 8 mà,nhưng mà phải vẽ hình mới giải đc,nhưng mk k bít vẽ hình ở trên đây ,nên chịu.THÔNG CẢM!!
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Vẽ tia Cx vuông góc với BC cắt tia phân giác goc B tại F, BF cắt AC tại E. Vẽ CD vuông góc với EF( D thuộc EF). Kéo dài AB cắt CD tại S. Chứng minh rằng:
a) CD là tia phân giác của góc ECF
b) DE=DF
c) SE//CF
Hình 4.16 có A ^ = 130 ° , C ^ = 140 ° và O A ⊥ O B . Chứng tỏ rằng AB // CD
Vì O A ⊥ O C nên A O C ^ = 90 ° . Trong góc AOC vẽ tia Ot sao cho O t / / A B .
Khi đó A ^ + A O t ^ = 180 ° (cặp góc trong cùng phía).
Suy ra A O t ^ = 180 ° − 130 ° = 50 ° .
Vì A O C ^ = 90 ° nên C O t ^ = 40 ° .
Ta có C ^ + C O t ^ = 140 ° + 40 ° = 180 ° .
Do đó CD // Ot (vì có cặp góc trong cùng phía bù nhau).
Suy ra AB // CD (vì cùng song song với Ot).
Đúng 0
Bình luận (0)
cho hình thang ABCD (AB//CD. góc C+góc D=90 độ, CD>AB. Gọi E, F thứ tự là trung điểm AB, CD. chứng minh EF=(CD-AB)/2
Hình 3.13 có
A
^
50
°
,
E
^
60
°
, góc
C
1
^
hơn góc
C
2
^
là
10
0
, góc
C
2
^
hơn góc ACE là ...
Đọc tiếp
Hình 3.13 có A ^ = 50 ° , E ^ = 60 ° , góc C 1 ^ hơn góc C 2 ^ là 10 0 , góc C 2 ^ hơn góc ACE là 10 0 . Chứng tỏ rằng A B / / C D;CD / / E F
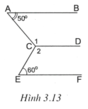
Đặt A C E ^ = m ° thì C 2 ^ = m ° + 10 ° và C 1 ^ = m ° + 20 ° .
Ta có A C E ^ + C 1 ^ + C 2 ^ = 360 ° do đó
m ° + m ° + 10 ° + m ° + 20 ° = 360 ° ⇒ 3 m ° + 30 ° = 360 ° ⇒ m ° = 110 ° .
Vậy C 2 ^ = 120 ° ; C 1 ^ = 130 ° .
Ta có A ^ + C 1 ^ = 50 ° + 130 ° = 180 ° ⇒ A B / / C D ; E ^ + C 2 ^ = 60 ° + 120 ° = 180 ° ⇒ C D / / E F ; vì có cặp góc trong cùng phía bù nhau.
Vận dụng nhiều dấu hiệu song song
Đúng 0
Bình luận (0)