Vẽ BO, kéo dài BO cắt AC tại D.

Ta có \(\widehat{BOC}=\widehat{BDC}+\widehat{DCO}\) và \(\widehat{BDC}=\widehat{A}+\widehat{ABD}\)

\(\Rightarrow\widehat{BOC}=\widehat{A}+\widehat{ABD}+\widehat{DCO}>\widehat{A}\)

a) Ta có: + \(\widehat{BOC}\)là góc ngoài của tam giác OBK

                 => \(\widehat{BOC}=\widehat{OBK}+\widehat{OKB}\)    (1)

               + \(\widehat{OKB}\)là góc ngoài của tam giác AKC

                  =>\(\widehat{OKB}=\widehat{A}+\widehat{ACK}\)(2)

Từ (1)(2) =>\(\widehat{BOC}=\widehat{OBK}+\widehat{A}+\widehat{ACK}\)

hay\(\widehat{BOC}=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)

b) Ta có:\(\widehat{ABO}+\widehat{ACO}=90^o-\frac{\widehat{A}}{2}\)

=>\(2\widehat{ABO}+2\widehat{ACO}=180^o-\widehat{A}\)(3)

 Xét tam giác ABC có:

\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)( Tổng 3 góc trong 1 tam giác)

=>\(\widehat{ABC}+\widehat{ACB}=180^o-\widehat{A}\)(4)

Từ (3)(4) => \(2\widehat{ABO}+2\widehat{ACO}=\widehat{ABC}+\widehat{ACB}\)(*)

Ta có: BO là tia phân giác của góc ACB

=>\(2\widehat{ABO}=\widehat{ABC}\)(**)

Từ (*)(**) => \(2\widehat{ABO}+2\widehat{ACO}=2\widehat{ABO}+\widehat{ACB}\)

=>\(2\widehat{ACO}=\widehat{ACB}\)

=> CO là tia phân giác của góc ACB

thank you

 Kéo dài tia AO và đặt là Ax. Khi đó:

\(\widehat{BOC}=\widehat{BOx}+\widehat{COx}\)

 Xét tam giác OAB có \(\widehat{BOx}\) là góc ngoài tại O nên 

\(\widehat{BOx}=\widehat{A_1}+\widehat{ABO}\) (1)

 Tương tự, ta có \(\widehat{COx}=\widehat{A_2}+\widehat{ACO}\) (2)

 Cộng theo vế (1) và (2), ta được:

 \(\widehat{BOC}=\widehat{A_1}+\widehat{A_2}+\widehat{ABO}+\widehat{ACO}\)

        \(=\widehat{A}+\widehat{ABO}+\widehat{ACO}\)

 Ta có đpcm.

a) (thay vô y như toán đại í )

t.g OBC có: O1^+B1^+C1^=180 độ => O1^=180 độ - B^1-C1^

t.g ABC có: A1^+B2^+B^1+C^2+C1^=180 độ

=> A1^+B^2+C^2=180 độ - B^1-C^1=O1^

=> BOC^=BAC^+ABO^+ACO^

b) B2^+C2^=90 độ - A1^:2 

=> B2^+C^2= 90 độ - (180 độ  - B1^ - B2^ - C1^ - C2^):2

=> B2^+C2^= 90 độ - 90 độ +(B1^+B2^+C2^+C1^):2

=> B2^+C2^=B2+(C1^+C2^):2 ( vì BO là tia p.g của ABC^)

=> C2^=(C1^+C2^):2 => CO là tia p/g của ACB^

có mấy cái t vt: B^1 tức là góc B1 đó, vt nhầm :((

HAY DAY CHANG TRAI TRE

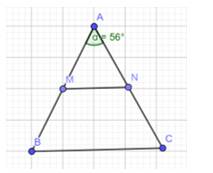
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)

Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)

b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )

Mà M, N là trung điểm của AB, AC

Nên AM = AN

Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A

\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)

c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)

Mà chúng ở vị trí đồng vị nên MN⫽BC

a: góc BOC=180 độ-góc OBC-góc OCB

=180 độ-(góc ABC-góc ABO)-(góc ACB-góc ACO)

=180 độ-góc ABC-góc ACB+góc ABO+góc ACO

=góc A+góc ABO+góc ACO

b: góc BOC=góc A+90 độ-1/2*góc A=90 độ+1/2*góc A

=>góc OBC+góc OCB=90 độ-1/2*góc A

=>góc ABC/2+góc OCB=(180 độ-góc BAC)/2

=>góc OCB=góc ACB/2

=>CO là phân giác của góc ACB