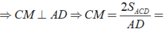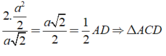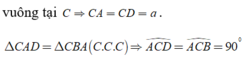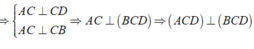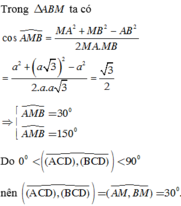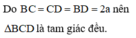cho tứ diện ABCD AB=AC=acăn2 BD=CD=acăn3 BC=2a góc tạo bởi mp (ABC) và (DBC) = 45 độ. khoảng cách từ B đến (ACD) là

Những câu hỏi liên quan
Cho tứ diện ABCD có các tam giác ABC và DBC vuông cân và nằm trong hai mặt phẳng vuông góc với nhau,
A
B
A
C
D
B
D
C
2
a
. Tính khoảng cách từ B đến mp (ACD) A.
a
6
B.
2
a
6
3
C.
a...
Đọc tiếp
Cho tứ diện ABCD có các tam giác ABC và DBC vuông cân và nằm trong hai mặt phẳng vuông góc với nhau, A B = A C = D B = D C = 2 a . Tính khoảng cách từ B đến mp (ACD)
A. a 6
B. 2 a 6 3
C. a 6 3
D. a 6 2
Đáp án là B.

B C = A B 2 = 2 a 2 .Gọi H là trung điểm BC ta có:
A H ⊥ B C B C = A B C ∩ D B C A B C ⊥ D B C ⇒ A H ⊥ D B C
kẻ H E ⊥ D C , H K ⊥ A E (1)
D C ⊥ H E D C ⊥ A H ( d o A H ⊥ D B C ⊂ D C ) ⇒ D C ⊥ A H E ⇒ D C ⊥ H K 2
từ 1 & 2 H K ⊥ A D C ⇒ d H ; A D C = H K
d B ; A D C = 2 d H ; A D C = 2 A H . H E A H 2 + H E 2 = 2 6 3
A H = B C 2 , H E = A B 2 ; A H = B C 2 = a 2 , H E = B C 2 = a
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
A
B
A
D
a
2
,
B
C
B
D
a
và
C
A
C
D
x
. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a...
Đọc tiếp
Cho tứ diện ABCD có A B = A D = a 2 , B C = B D = a và C A = C D = x . Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 0 .
B. 45 0 .
C. 90 0 .
D. 120 0 .
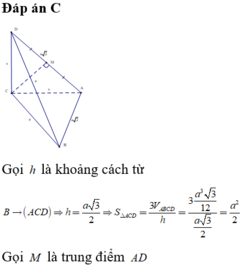
Đáp án C
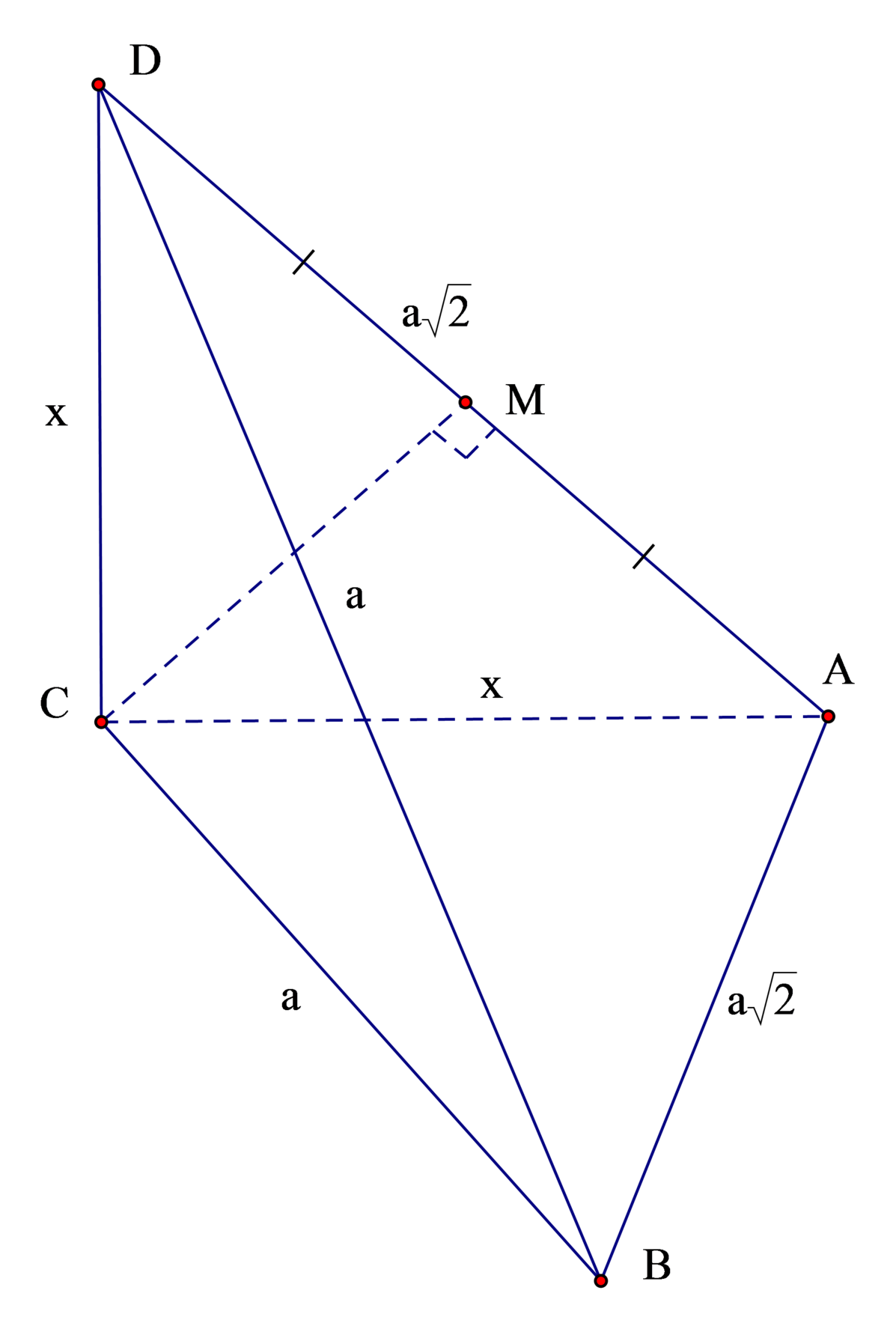
Gọi h là khoảng cách từ B → A C D
⇒ h = a 3 2 ⇒ S Δ A C D = 3 V A B C D h = 3 a 3 3 12 a 3 2 = a 2 2
Gọi M là trung điểm AD ⇒ C M ⊥ A D .
⇒ C M = 2 S A C D A D = 2. a 2 2 a 2 = a 2 2 = 1 2 A D
⇒ Δ A C D vuông tại C ⇒ C A = C D = a
Δ C A D = Δ C B A C . C . C ⇒ A C D ^ = A C B ^ = 90 0
⇒ A C ⊥ C D A C ⊥ C B ⇒ A C ⊥ B C D ⇒ A C D ⊥ B C D
Hay góc giữa hai mặt phẳng bằng 90 0
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có ABAD
a
2
, BCBDa, CACDx. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là A.
60
o...
Đọc tiếp
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o
Cho tứ diện ABCD có AB AD a
2
, BC BD a và CA CD x. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là: A.600 B.450 C.900 D.1200
Đọc tiếp
Cho tứ diện ABCD có AB = AD = a 2 , BC = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A.600
B.450
C.900
D.1200
Chọn C
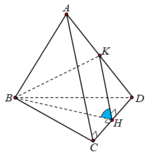
Gọi H là trung điểm cạnh CD và K là trung điểm cạnh AD.
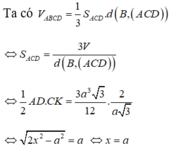
Tam giác ACD có CA=CD=x=a ; AD = a 2 => tam giác ACD vuông cân tại C
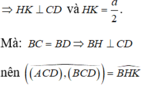
Mặt khác:
Tam giác ABD có:
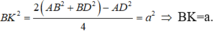
Tam giác BHK có:
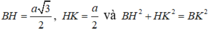
=> Tam giác BHK vuông tại H ⇒ B H K ^ = 90 o hay A C D , B C D ^ = 90 o
Đúng 0
Bình luận (0)
Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có
A
B
2
a
,
A
C
D
60
o
. M là trung điểm AB,
N
∈
B
C...
Đọc tiếp
Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có A B = 2 a , A C D = 60 o . M là trung điểm AB, N ∈ B C sao cho . Khi đó khoảng cách từ P đến mặt phẳng (BCD) bằng (với P là giao điểm MN và AC).
A. 2 a 21 7 .
B. a 21 7 .
C. a 7 7
D. 2 a 7 7
Đáp án A
Chọn hệ trục tọa độ Oxy
![]()
A D = 2 a tan 60 o = 2 a 3
Từ M kẻ MH song song với AC ta có MH =a
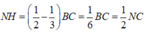
![]()
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1
Vậy khoảng cách từ
P
(
0
;
4
a
;
0
)
đến (BCD) là:
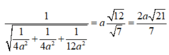
Đúng 0
Bình luận (0)
Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có AB 2a,
A
C
D
60
o
. M là trung điểm AB,
N
∈
B
C
sao cho BN 2NC. Khi đó khoảng cách từ P đến mặt phẳng (BCD) bằng (với P là giao điểm MN và AC) A.
2
a
21...
Đọc tiếp
Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có AB = 2a, A C D = 60 o . M là trung điểm AB, N ∈ B C sao cho BN = 2NC. Khi đó khoảng cách từ P đến mặt phẳng (BCD) bằng (với P là giao điểm MN và AC)
A. 2 a 21 7
B. a 21 7
C. a 7 7
D. 2 a 7 7
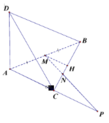
Chọn hệ trục tọa độ Oxyz. Có O = A, AB = Ox, AC = Oy, AD = Oz, AD = 2 α tan 60 o = 2 a 3 , N H = 1 2 - 1 3 B C = 1 6 B C = 1 2 N C
Từ M kẻ MH song song với AC ta có MH = a; CP = 2MH = 2a ⇒ AP = 4a
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1 . Vậy khoảng cách từ P ( 0;4a;0 ) đến (BCD) là:
1 1 4 a 2 + 1 4 a 2 + 1 12 a 2 = a 12 7 = 2 a 21 7
Đáp án cần chọn là A
Đúng 0
Bình luận (0)
Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có
A
B
2
a
,
A
C
D
60
°
. M là trung điểm AB,
N
∈
B
C
sao cho
B
N
→
2
N
C
→
. Khi đó khoảng cách từ P đến mặt phẳng (BCD)...
Đọc tiếp
Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có A B = 2 a , A C D = 60 ° . M là trung điểm AB, N ∈ B C sao cho B N → = 2 N C → . Khi đó khoảng cách từ P đến mặt phẳng (BCD) bằng (với P là giao điểm MN và AC)
A. 2 a 21 7
B. a 21 7
C. a 7 7
D. 2 a 7 7
Cho tứ diện ABCD có
B
C
C
D
B
D
2
a
,
A
C
a
2
,
A
B
a
.
Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là A. 90o. B. 60o. C. 45o. D. 30o.
Đọc tiếp
Cho tứ diện ABCD có B C = C D = B D = 2 a , A C = a 2 , A B = a . Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là
A. 90o.
B. 60o.
C. 45o.
D. 30o.
Cho tứ diện ABCD có
B
C
C
D
B
D
2
a
,
A
C
A
D
a
2
,
A
B
a
. Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là: A.
90
°
B.
60
°
C.
45
°
D.
30
°
Đọc tiếp
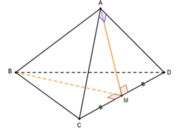
Cho tứ diện ABCD có B C = C D = B D = 2 a , A C = A D = a 2 , A B = a . Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là:
A. 90 °
B. 60 °
C. 45 °
D. 30 °