Question

Tứ diện ABCD có AB, AC, AD đôi một vuông góc. Tam giác ABC cân tại A, có AB = 2a, A C D = 60 o . M là trung điểm AB, N ∈ B C sao cho BN = 2NC. Khi đó khoảng cách từ P đến mặt phẳng (BCD) bằng (với P là giao điểm MN và AC)

A.  2 a 21 7

B.  a 21 7

C.  a 7 7

D.  2 a 7 7

Answer 1

 

 

 

 

 

 

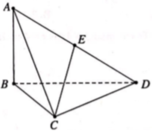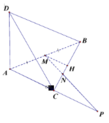
Chọn hệ trục tọa độ Oxyz. Có O = A, AB = Ox, AC = Oy, AD = Oz, AD = 2 α tan 60 o = 2 a 3 , N H = 1 2 - 1 3 B C = 1 6 B C = 1 2 N C

Từ M kẻ MH song song với AC ta có MH = a; CP = 2MH = 2a ⇒ AP = 4a

PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1 . Vậy khoảng cách từ P ( 0;4a;0 ) đến (BCD) là:

1 1 4 a 2 + 1 4 a 2 + 1 12 a 2 = a 12 7 = 2 a 21 7

Đáp án cần chọn là A