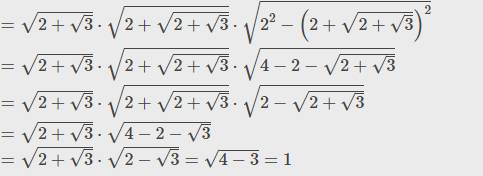cho A=\(\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+......+\dfrac{1}{\sqrt{20}+\sqrt{21}}\)

Những câu hỏi liên quan
Thực hiện các phép tính :
1. \(A=\sqrt{2-\sqrt{3}}\sqrt{2+\sqrt{2-\sqrt{3}}}\sqrt{2+\sqrt{2+\sqrt{2-\sqrt{3}}}}\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2-\sqrt{3}}}}}\)
2. \(B=\left(\dfrac{1}{1+\sqrt{2}}+\dfrac{2}{2+\sqrt{3}}+...+\dfrac{1}{20+\sqrt{21}}\right)\cdot2022\)
Giải chi tiết giúp mình ạ
1:
\(A=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2^2-\left(2+\sqrt{2-\sqrt{3}}\right)}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2-\sqrt{2-\sqrt{3}}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{4-2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
Đúng 0
Bình luận (0)
Tính : \(\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{2+\sqrt{3}}+...+\dfrac{1}{20+\sqrt{21}}\)
\(1=2-1=\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)\)=>\(\dfrac{1}{1+\sqrt{2}=}=\dfrac{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}{1+\sqrt{2}}=\sqrt{2}-1\)
cmtt thì biểu thức thành
\(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+...+\sqrt{21}-\sqrt{20}\)=\(1+\sqrt{21}\)
Đúng 0
Bình luận (1)
Tính :
a) dfrac{5+2sqrt{5}}{sqrt{5}}+dfrac{3+sqrt{3}}{sqrt{3}}-left(sqrt{5}+sqrt{3}right)
b) left(dfrac{1}{2-sqrt{5}}+dfrac{2}{sqrt{5}+sqrt{3}}right):dfrac{1}{sqrt{21+12sqrt{3}}}
c) dfrac{sqrt{2}+sqrt{3}+sqrt{4}}{sqrt{2}+sqrt{3}+sqrt{6}+sqrt{8}+4}
d) sqrt{21-6sqrt{6}}+sqrt{9+2sqrt{18}}-2sqrt{6+3sqrt{3}}
e) sqrt{6+2sqrt{5-sqrt{13+sqrt{48}}}}
f) dfrac{left(5+2sqrt{6}right)left(49-20sqrt{6}right)left(sqrt{5-2sqrt{6}}right)}{9sqrt{3}-11sqrt{2}}
g) left(dfrac{1-asqrt{a}}{1-sqrt{a}}+sqrt{a}righ...
Đọc tiếp
Tính :
a) \(\dfrac{5+2\sqrt{5}}{\sqrt{5}}+\dfrac{3+\sqrt{3}}{\sqrt{3}}-\left(\sqrt{5}+\sqrt{3}\right)\)
b) \(\left(\dfrac{1}{2-\sqrt{5}}+\dfrac{2}{\sqrt{5}+\sqrt{3}}\right):\dfrac{1}{\sqrt{21+12\sqrt{3}}}\)
c) \(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}\)
d) \(\sqrt{21-6\sqrt{6}}+\sqrt{9+2\sqrt{18}}-2\sqrt{6+3\sqrt{3}}\)
e) \(\sqrt{6+2\sqrt{5-\sqrt{13+\sqrt{48}}}}\)
f) \(\dfrac{\left(5+2\sqrt{6}\right)\left(49-20\sqrt{6}\right)\left(\sqrt{5-2\sqrt{6}}\right)}{9\sqrt{3}-11\sqrt{2}}\)
g) \(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)-\dfrac{\left(1-\sqrt{a}\right)^2}{\left(1-a\right)^2}\)
a: \(=\sqrt{5}+2+\sqrt{3}+1-\sqrt{5}-\sqrt{3}=3\)
b: \(=\left(-\sqrt{5}-2+\sqrt{5}-\sqrt{3}\right)\cdot\left(2\sqrt{3}+3\right)\)
\(=-\sqrt{3}\left(2+\sqrt{3}\right)\cdot\left(2+\sqrt{3}\right)\)
\(=-\sqrt{3}\left(7+4\sqrt{3}\right)=-7\sqrt{3}-12\)
c: \(=\dfrac{\sqrt{2}+\sqrt{3}+2}{\left(\sqrt{2}+\sqrt{3}+2\right)+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+2\right)}=\dfrac{1}{1+\sqrt{2}}=\sqrt{2}-1\)
Đúng 0
Bình luận (0)
rút gọn
a)sqrt{20}+sqrt{80}-sqrt{45}
b)4.sqrt{dfrac{2}{9}}+sqrt{2}+sqrt{dfrac{1}{18}}
c)dfrac{1}{sqrt{3}-1}-dfrac{1}{sqrt{3}+1}
d)dfrac{1}{sqrt{x}-1}-dfrac{1}{sqrt{x}+1}+1
e)sqrt{x}-2+dfrac{10-x}{sqrt{x}+2}
g)dfrac{1}{sqrt{x}+2}-dfrac{2}{sqrt{x}-2}-dfrac{sqrt{x}}{4-x}
Đọc tiếp
rút gọn
a)\(\sqrt{20}\)+\(\sqrt{80}\)-\(\sqrt{45}\)
b)4.\(\sqrt{\dfrac{2}{9}}\)+\(\sqrt{2}\)+\(\sqrt{\dfrac{1}{18}}\)
c)\(\dfrac{1}{\sqrt{3}-1}\)-\(\dfrac{1}{\sqrt{3}+1}\)
d)\(\dfrac{1}{\sqrt{x}-1}\)-\(\dfrac{1}{\sqrt{x}+1}\)+1
e)\(\sqrt{x}\)-2+\(\dfrac{10-x}{\sqrt{x}+2}\)
g)\(\dfrac{1}{\sqrt{x}+2}\)-\(\dfrac{2}{\sqrt{x}-2}\)-\(\dfrac{\sqrt{x}}{4-x}\)
a: \(\sqrt{20}+\sqrt{80}-\sqrt{45}\)
\(=2\sqrt5+4\sqrt5-3\sqrt5\)
\(=6\sqrt5-3\sqrt5=3\sqrt5\)
b: \(4\cdot\sqrt{\frac29}+\sqrt2+\sqrt{\frac{1}{18}}\)
\(=4\cdot\frac{\sqrt2}{3}+\sqrt2+\sqrt{\frac{2}{36}}\)
\(=\frac43\sqrt2+\sqrt2+\frac16\sqrt2=\sqrt2\left(\frac43+1+\frac16\right)=\sqrt2\left(\frac86+\frac16+1\right)=\frac{15}{6}\cdot\sqrt2=\frac52\sqrt2\)
c: \(\frac{1}{\sqrt3-1}-\frac{1}{\sqrt3+1}\)
\(=\frac{\sqrt3+1-\left(\sqrt3-1\right)}{\left(\sqrt3+1\right)\left(\sqrt3-1\right)}\)
\(=\frac{\sqrt3+1-\sqrt3+1}{2}=\frac22=1\)
d: \(\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}+1\)
\(=\frac{\sqrt{x}+1-\left(\sqrt{x}-1\right)-\left(x-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{\sqrt{x}+1-\sqrt{x}+1-x+1}{x-1}=\frac{-x+3}{x-1}\)
e: \(\sqrt{x}-2+\frac{10-x}{\sqrt{x}+2}\)
\(=\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)+10-x}{\sqrt{x}+2}\)
\(=\frac{x-4+10-x}{x-4}=\frac{6}{x-4}\)
g: \(\frac{1}{\sqrt{x}+2}-\frac{2}{\sqrt{x}-2}-\frac{\sqrt{x}}{4-x}\)
\(=\frac{1}{\sqrt{x}+2}-\frac{2}{\sqrt{x}-2}+\frac{\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{\sqrt{x}-2-2\left(\sqrt{x}+2\right)+\sqrt{x}}{x-4}=\frac{2\sqrt{x}-2-2\sqrt{x}-4}{x-4}=\frac{-6}{x-4}\)
Đúng 0
Bình luận (0)
gptr:
1, \(\dfrac{x}{\sqrt{2x-1}}+\dfrac{1}{\sqrt[4]{4x-3}}=\dfrac{2}{x}\)
2, \(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}=\sqrt{3}\left(\dfrac{1}{\sqrt{4x-1}}+\dfrac{1}{\sqrt{5x-2}}\right)\)
3,\(\sqrt{-x^2+4x+21}-\sqrt{-x^2+3x+10}=\sqrt{2}\)
Éttttt ooooo éttttt. mời các thiên tài toán học ạ
1: ĐKXĐ: x>1/2
=>\(\dfrac{x}{\sqrt{2x-1}}+\dfrac{x}{\sqrt[4]{4x-3}}=2\)
x^2-2x+1>=0
=>x^2>=2x-1
=>\(\dfrac{x}{\sqrt{2x-1}}>=1\)
Dấu = xảy ra khi x=1
(x^2-2x+1)(x^2+2x+3)>=0
=>x^4-4x+3>=0
=>x^4>=4x-3
=>\(\dfrac{x}{\sqrt[4]{4x-3}}>=1\)
=>VT>=2
Dấu = xảy ra khi x=1
2: 4x-1=x+x+2x-1
5x-2=x+2x-1+2x-1
\(\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}\right)\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)>=9\)
=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{9}{\sqrt{x}+\sqrt{x}+\sqrt{2x-1}}\)
\(\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)^2< =3\left(4x-1\right)\)
=>\(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}< =\sqrt{3\left(4x-1\right)}\)
=>\(\dfrac{2}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{4x-1}}\)
Tương tự, ta cũng có: \(\dfrac{1}{\sqrt{x}}+\dfrac{2}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{5x-2}}\)
=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\sqrt{3}\left(\dfrac{1}{\sqrt{4x-1}}+\dfrac{1}{\sqrt{5x-2}}\right)\)
Dấu = xảy ra khi x=1
Đúng 2
Bình luận (1)
Adfrac{sqrt{x}+2}{sqrt{x}-2}-dfrac{3}{sqrt{x}+2}+dfrac{12}{x-4}Bdfrac{sqrt{x}}{sqrt{x}-3}-dfrac{sqrt{x}-21}{9-x}dfrac{1}{sqrt{x}+3}Cdfrac{sqrt{x}}{sqrt{x}+3}+dfrac{2sqrt{x}}{sqrt{x}-3}-dfrac{3x+9}{x-9}Ddfrac{1}{sqrt{x}+3}-dfrac{sqrt{x}}{3-sqrt{x}}+dfrac{2sqrt{x}+12}{x-9}Ndfrac{sqrt{x}}{sqrt{x}-1}+dfrac{2sqrt{x}-1}{sqrt{x}+1}-dfrac{6}{x-1}Mdfrac{3}{sqrt{x}-3}+dfrac{2}{sqrt{x}+3}+dfrac{x-5sqrt{x}-3}{x-9}
Đọc tiếp
\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}+\dfrac{12}{x-4}\)
\(B=\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{\sqrt{x}-21}{9-x}\dfrac{1}{\sqrt{x}+3}\)
\(C=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(D=\dfrac{1}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}+\dfrac{2\sqrt{x}+12}{x-9}\)
\(N=\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{6}{x-1}\)
\(M=\dfrac{3}{\sqrt{x}-3}+\dfrac{2}{\sqrt{x}+3}+\dfrac{x-5\sqrt{x}-3}{x-9}\)
a: Ta có: \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}+\dfrac{12}{x-4}\)
\(=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6+12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+\sqrt{x}+22}{x-4}\)
d: Ta có: \(D=\dfrac{1}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}+\dfrac{2\sqrt{x}-12}{x-9}\)
\(=\dfrac{\sqrt{x}-3+x+3\sqrt{x}+2\sqrt{x}-12}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+6\sqrt{x}-15}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
Đúng 0
Bình luận (0)
A=\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-\dfrac{3}{\sqrt{x}+2}+\dfrac{12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}A=\dfrac{\sqrt{x}+2.\left(\sqrt{x}+2\right)-3.\left(\sqrt{x}-2\right)+12}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}A=\dfrac{\sqrt{x}+2\sqrt{x}+4-3\sqrt{x}+6+12}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}A=\dfrac{22}{\left(\sqrt{x}-2\right).\left(\sqrt{x}+2\right)}\)
Đúng 0
Bình luận (0)
Bài 1 : Tính :
a) dfrac{1}{5+2sqrt{6}}-dfrac{1}{5-2sqrt{6}}
b) sqrt{6+2sqrt{5}}-dfrac{sqrt{15}-sqrt{3}}{sqrt{3}}
c) dfrac{3sqrt{2}-2sqrt{3}}{sqrt{3}-sqrt{2}}:dfrac{1}{sqrt{16}}
d) dfrac{3+2sqrt{3}}{sqrt{3}}+dfrac{2+sqrt{2}}{1+sqrt{2}}-dfrac{1}{2-sqrt{3}}
e) dfrac{4}{1+sqrt{3}}-dfrac{sqrt{15}+sqrt{3}}{1+sqrt{5}}
f) left(dfrac{1}{2-sqrt{5}}+dfrac{2}{sqrt{5}-sqrt{3}}right):dfrac{1}{sqrt{21-12sqrt{3}}}
Bài 2 : Rút gọn :
a) dfrac{a+b-2sqrt{ab}}{sqrt{a}-sqrt{b}}:dfrac{1}{sqrt{a}+sqrt{b}}
b) l...
Đọc tiếp
Bài 1 : Tính :
a) \(\dfrac{1}{5+2\sqrt{6}}-\dfrac{1}{5-2\sqrt{6}}\)
b) \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\)
c) \(\dfrac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\)
d) \(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
e) \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\)
f) \(\left(\dfrac{1}{2-\sqrt{5}}+\dfrac{2}{\sqrt{5}-\sqrt{3}}\right):\dfrac{1}{\sqrt{21-12\sqrt{3}}}\)
Bài 2 : Rút gọn :
a) \(\dfrac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}\)
b) \(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right).\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
c) \(\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
(bài 1) a) \(\dfrac{1}{5+2\sqrt{6}}-\dfrac{1}{5-2\sqrt{6}}\) = \(\dfrac{5-2\sqrt{6}-5-2\sqrt{6}}{25-24}\)
= \(\dfrac{-4\sqrt{6}}{1}\) = \(-4\sqrt{6}\)
b) \(\sqrt{6+2\sqrt{5}}-\dfrac{\sqrt{15}-\sqrt{3}}{\sqrt{3}}\) = \(\sqrt{\left(\sqrt{5}+1\right)^2}-\dfrac{\sqrt{3}\left(\sqrt{5}-1\right)}{\sqrt{3}}\)
= \(\left(\sqrt{5}+1\right)-\left(\sqrt{5}-1\right)\) = \(\sqrt{5}+1-\sqrt{5}+1\) = \(2\)
c) \(\dfrac{3\sqrt{2}-2\sqrt{3}}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\) = \(\dfrac{\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}:\dfrac{1}{\sqrt{16}}\)
= \(\sqrt{6}.\sqrt{16}\) = \(4\sqrt{6}\)
d) \(\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{1+\sqrt{2}}-\dfrac{1}{2-\sqrt{3}}\)
= \(\sqrt{3}+2+\sqrt{2}-\dfrac{1}{2-\sqrt{3}}\) = \(\dfrac{\left(\sqrt{3}+2+\sqrt{2}\right)\left(2-\sqrt{3}\right)-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{3}-3+4-2\sqrt{3}+2\sqrt{2}-\sqrt{6}-1}{2-\sqrt{3}}\)
= \(\dfrac{2\sqrt{2}-\sqrt{6}}{2-\sqrt{3}}\) = \(\dfrac{\sqrt{2}\left(2-\sqrt{3}\right)}{2-\sqrt{2}}\) = \(\sqrt{2}\)
e) \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{15}+\sqrt{3}}{1+\sqrt{5}}\) = \(\dfrac{4}{1+\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{5}+1\right)}{1+\sqrt{5}}\)
= \(\dfrac{4}{1+\sqrt{3}}-\sqrt{3}\) = \(\dfrac{4-\sqrt{3}-3}{1+\sqrt{3}}\) = \(\dfrac{1-\sqrt{3}}{1+\sqrt{3}}\)
= \(\dfrac{\left(1-\sqrt{3}\right)\left(1-\sqrt{3}\right)}{1-3}\) = \(\dfrac{1-2\sqrt{3}+3}{-2}\) = \(\dfrac{4-2\sqrt{3}}{-2}\)
= \(\dfrac{-2\left(-2+\sqrt{3}\right)}{-2}\) = \(\sqrt{3}-2\)
Đúng 0
Bình luận (0)
bài 2)
a)\(\dfrac{a+b-2\sqrt{ab}}{\sqrt{a}-\sqrt{b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}=\dfrac{\left(a+b-2\sqrt{ab}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+a\sqrt{b}+b\sqrt{a}+b\sqrt{b}-2a\sqrt{b}-2b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{a\sqrt{a}+-a\sqrt{b}+b\sqrt{b}-b\sqrt{a}}{\sqrt{a}-\sqrt{b}}\) = \(\dfrac{a\left(\sqrt{a}-\sqrt{b}\right)-b\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
= \(\dfrac{\left(a-b\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\) = \(a-b\)
b) \(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right).\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)^2-\sqrt{a}\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{\sqrt{a}\left(a-2\sqrt{a}+1\right)-\sqrt{a}\left(a+2\sqrt{a}+1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2a-2}{4\sqrt{a}}.\dfrac{a\sqrt{a}-2a+\sqrt{a}-a\sqrt{a}-2a-\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)
= \(\dfrac{2\left(a-1\right)}{4\sqrt{a}}.\dfrac{-4a}{a-1}\) = \(-2\)
Đúng 0
Bình luận (0)
Tính: a, \(\left(4\sqrt{2}-\dfrac{11}{2}\sqrt{8}-\dfrac{1}{3}\sqrt{288}+\sqrt{50}\right)\left(\dfrac{1}{2}\sqrt{2}\right)\)
b, \(\left(\dfrac{4}{5}\sqrt{5}-\dfrac{1}{3}\sqrt{\dfrac{1}{5}}+3\sqrt{20}+\dfrac{1}{2}\sqrt{245}\right)\div\sqrt{5}\)
a: Ta có: \(\left(4\sqrt{2}-\dfrac{11}{2}\sqrt{8}-\dfrac{1}{3}\sqrt{288}+\sqrt{50}\right)\cdot\left(\dfrac{1}{2}\sqrt{2}\right)\)
\(=\dfrac{1}{2}\sqrt{2}\cdot\left(4\sqrt{2}-11\sqrt{2}-4\sqrt{2}+5\sqrt{2}\right)\)
\(=\dfrac{1}{2}\sqrt{2}\cdot6\sqrt{2}=3\)
Đúng 1
Bình luận (0)
dfrac{2sqrt{3}-3sqrt{2}}{sqrt{6}}-dfrac{2}{1-sqrt{3}}dfrac{4}{sqrt{6}+sqrt{2}}-dfrac{sqrt{54}+sqrt{2}}{sqrt{3}+1}dfrac{5+2sqrt{5}}{sqrt{5}}-dfrac{20}{5+sqrt{5}}-sqrt{20}Bài 2sqrt{25x^2-10x+1}sqrt{4x^2+8x+4}sqrt{x^2-3}+1xsqrt{7-2x}sqrt{x^2+7}sqrt{9x-27}+dfrac{1}{2}sqrt{4x-12}-9sqrt{dfrac{x-3}{9}}2
Đọc tiếp
\(\dfrac{2\sqrt{3}-3\sqrt{2}}{\sqrt{6}}-\dfrac{2}{1-\sqrt{3}}\)
\(\dfrac{4}{\sqrt{6}+\sqrt{2}}-\dfrac{\sqrt{54}+\sqrt{2}}{\sqrt{3}+1}\)
\(\dfrac{5+2\sqrt{5}}{\sqrt{5}}-\dfrac{20}{5+\sqrt{5}}-\sqrt{20}\)
Bài 2
\(\sqrt{25x^2-10x+1}=\sqrt{4x^2+8x+4}\)
\(\sqrt{x^2-3}+1=x\)
\(\sqrt{7-2x}=\sqrt{x^2+7}\)
\(\sqrt{9x-27}+\dfrac{1}{2}\sqrt{4x-12}-9\sqrt{\dfrac{x-3}{9}}=2\)
\(2,\\ a,PT\Leftrightarrow\sqrt{\left(5x-1\right)^2}=\sqrt{4\left(x+1\right)^2}\\ \Leftrightarrow\left|5x-1\right|=2\left|x+1\right|\\ \Leftrightarrow\left[{}\begin{matrix}5x-1=2\left(x+1\right)\\1-5x=2\left(x+1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=3\\7x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{7}\end{matrix}\right.\)
\(b,ĐK:x^2-3\ge0\\ PT\Leftrightarrow\sqrt{x^2-3}=x-1\\ \Leftrightarrow x^2-3=x^2-2x+1\\ \Leftrightarrow2x=4\Leftrightarrow x=2\left(tm\right)\\ c,ĐK:x\le\dfrac{7}{2}\\ PT\Leftrightarrow7-2x=x^2+7\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\\ d,ĐK:x\ge3\\ PT\Leftrightarrow3\sqrt{x-3}+\dfrac{1}{2}\cdot2\sqrt{x-3}-9\cdot\dfrac{1}{3}\sqrt{x-3}=2\\ \Leftrightarrow\sqrt{x-3}=2\\ \Leftrightarrow x-3=4\Leftrightarrow x=7\left(tm\right)\)
Đúng 2
Bình luận (1)
Bài 1:
d: Ta có: \(\dfrac{5+2\sqrt{5}}{\sqrt{5}}-\dfrac{20}{5+\sqrt{5}}-\sqrt{20}\)
\(=\sqrt{5}+2-5+\sqrt{5}-2\sqrt{5}\)
=-3
Đúng 1
Bình luận (1)