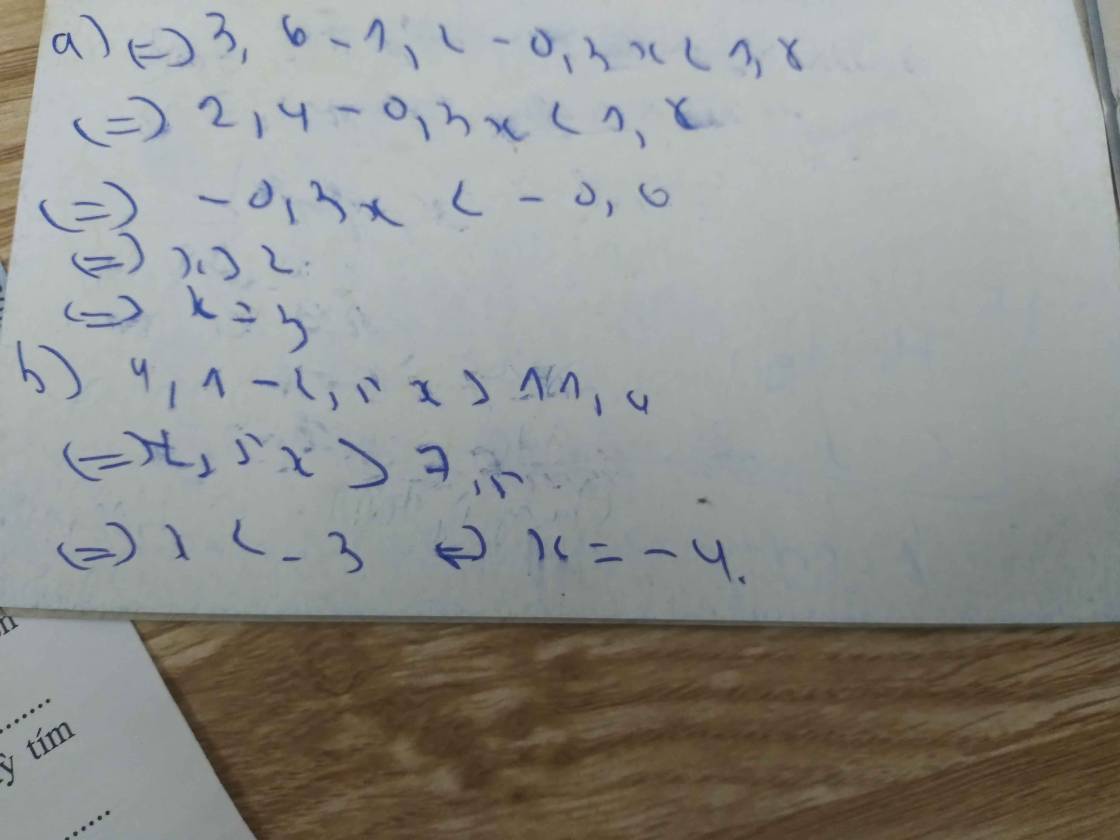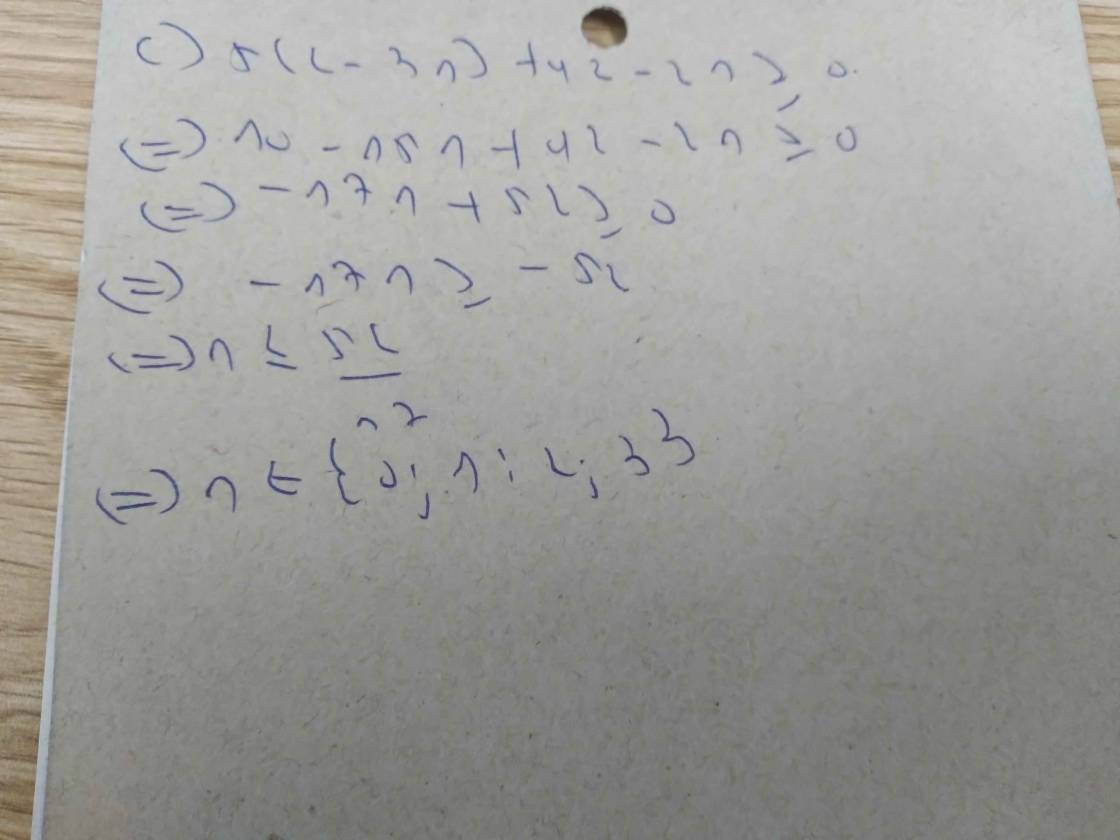Tìm số nguyên dương n lớn nhất sao cho \(\dfrac{n^2+2n+1}{n+23}\) là một số nguyên .

Những câu hỏi liên quan
Tìm số nguyên dương lớn nhất sao cho n2+2n+1 / n+23 có giá trị nguyên
tìm số nguyên dương n lớn nhất sao cho n2+2n+1 phần n+23 có giá trị nguyên
Muốn \(\frac{n^2+2n+1}{n+23}\) có giá trị nguyên thì:
\(n^2+2n+1⋮n+23\Rightarrow n^2+2n+1-n.\left(n+23\right)⋮n+23\)
\(\Rightarrow n^2+2n+1-n^2-23n⋮n+23\)
\(\Rightarrow-21n+1⋮n+23\Rightarrow-21n+1+21\left(n+23\right)⋮n+23\)
\(\Rightarrow-21n+1+21n+23⋮n+23\)
\(\Rightarrow24⋮n+23\Rightarrow n+23\inƯ\left(24\right)\)
Mà n lớn nhất nên: n+23 lớn nhất => n+23 = 24 => n=1
Vậy n = 1
Đúng 0
Bình luận (0)
Cho mình xin lỗi:
\(-21n+1⋮n+23\Rightarrow-21n+1+21\left(n+23\right)⋮n+23\)
\(\Rightarrow-21n+1+21n+483⋮n+23\Rightarrow484⋮n+23\)
Mà n là số nguyên dương lớn nhất nên: n+23=484 => n = 461
Vậy n = 461
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm số nguyên dương n lớn nhất sao cho \(\frac{n^2+2n+1}{n+23}\) có giá trị nguyên
Tìm số nguyên dương lớn nhất sao cho n^2+2n+1/n+23 có giá trị nguyên.
Giúp mk có cả lời giải nhé! Mk sẽ tick!!~~
Mk lam tu luc nay gio matu nhien no biến mất .
Bang461 nhe
Đúng 0
Bình luận (0)
Tìm n nguyên dương lớn nhất sao cho:
\(\frac{n^2+2n+1}{n+23}\)
Ta có :
\(\frac{n^2+2n+1}{n+23}\in Z\Rightarrow n^2+2n+1⋮n+23\)
\(\Rightarrow n^2+23n-\left(21n-1\right)⋮n+23\)
\(\Rightarrow n\left(n+23\right)-\left(21n-1\right)⋮n+23\)
Mà \(n\left(n+23\right)⋮n+23\)
\(\Rightarrow21n-1⋮n+23\)
\(\Rightarrow21n+483-484⋮n+23\)
\(\Rightarrow21\left(n+23\right)-484⋮n+23\)
,Mà \(21\left(n+23\right)⋮n+23\)
\(\Rightarrow484⋮n+23\)
Vậy n lớn nhất \(\Leftrightarrow n+23=484\)
\(\Leftrightarrow n=461\)
bài 5 :
a, tìm số nguyên dương nhỏ nhất sao cho ; 3,6 - (1,2+0,3x) <1,8
b, tìm số nguyên âm lớn nhất sao cho : 4,1 - 2,5x > 11,6
c, tìm số tự nhiên n sao cho ; 5(2-3n) + 42 - 2n > hoặc bằng 0
Cho biểu thức A= \(\dfrac{2n+1}{n-2}\)
a) Tìm điều kiện của số nguyên n để A là một phân số. Tính giá trị của A khi n= -2.
b)Tìm các số nguyên n sao cho phân số A có giá trị là một số nguyên.
a: Để A là phân số thì n-2<>0
=>n<>2
Khi n=-2 thì \(A=\dfrac{2\cdot\left(-2\right)+1}{-2-2}=\dfrac{-3}{-4}=\dfrac{3}{4}\)
b: Để A nguyên thì 2n+1 chia hết cho n-2
=>2n-4+5 chia hết cho n-2
=>\(n-2\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{3;1;7;-3\right\}\)
Đúng 2
Bình luận (0)
Tìm số nguyên ''n'' sao cho :n - 2015 ;n - 14;n - 6 là các số nguyên tốtìm các số nguyên ''n'' sao cho ;4n+9/2n+3 có giá trị lớn nhấtcho phân số a/b tối giản. Chứng minh phân số 5a+3b/13a+8bTìm ba số nguyên dương khác nhausao cho tổng nghịch đảo của chúng=1
Tìm số nguyên dương lớn nhất để : A = n3 -2n3 +3 / n- 2 là số nguyên