c/m1:

gọi O là giao điểm của 2 đường chéo trong tứ giác , gọi tên của tứ giác đó là tứ giác  ABCD:

Trong Δ OAB có :

OA+OB>AB

Trong Δ OBC có :

OB+OC>BC 

Trong Δ OAD có :

OD+OA>AD

Trong Δ OCD có :

OC+OD>CD

Ta có 4 bất đẳng thức:

2OB+2OC+2OA+2OD<AB+BC+CD+DA

<=>2BD+2AC>1/2p

<=>BD+AC> 1/2p

Vậy tổng 2 đường chéo trong 1 tứ giác luôn lớn hơn nửa chu vi (đpcm)

p : là nửa chu vi

c/m2:

Vẫn sử dụng tứ giác ABCD 

do AC<p và BD<p

<=>AC+BD<2p

vậy tổng 2 đường chéo nhỏ hơn chu vi của tứ giác(đpcm)

Dùng bất đẳng thức tam giác bạn ơi

Gọi O là giao của AC và BD

AB>AO+BO

AD>AO+DO

BC>BO+CO

DC>DO+CO

=>AB+AD+BC+CD>2(AC+BD)

=>(AC+BD)<P/2

AC<AB+BC

AC<AD+DC

BD<BC+CD

BD<AB+AD

=>2(AC+BD)<2*C ABCD

=>AC+BD<C ABCD

Gọi O là giao điểm 2 dường chéo AC và BD của tứ giác ABCD.
Áp dụng định lý " trong một tam giác một cạnh thì bé hơn tổng 2 cạnh kia" ta có:
AB < OA + OB (1)
BC < OB + OC (2)
CD < OC + OD (3)
DA < OD + OA (4)
(1) + (2) + (3) + (4) :
AB + BC + CD + DA < 2(OA + OC + OB + OD) = 2(AC + BD)
hay (1/2)(AB + BC + CD + DA) < AC + BD (*)
Mặt khác :
AC < AB + BC (1')
BD < BC + CD (2')
AC < CD + DA (3')
BD < DA + AB (4')
(1') + (2') + (3') + (4') :
2(AC + BD) > 2(AB + BC + CD + DA)
hay AC + BD < AB + BC + CD + DA (**)
Từ (*) và (**) (1/2)(AB + BC + CD + DA) < AC + BD < AB + BC + CD + DA

Gọi O là giao điểm 2 dường chéo AC và BD của tứ giác ABCD.
Áp dụng định lý " trong một tam giác một cạnh thì bé hơn tổng 2 cạnh kia" ta có:
AB < OA + OB (1)
BC < OB + OC (2)
CD < OC + OD (3)
DA < OD + OA (4)
(1) + (2) + (3) + (4) :
AB + BC + CD + DA < 2(OA + OC + OB + OD) = 2(AC + BD)
hay (1/2)(AB + BC + CD + DA) < AC + BD (*)
Mặt khác :
AC < AB + BC (1')
BD < BC + CD (2')
AC < CD + DA (3')
BD < DA + AB (4')
(1') + (2') + (3') + (4') :
2(AC + BD) > 2(AB + BC + CD + DA)
hay AC + BD < AB + BC + CD + DA (**)
Từ (*) và (**) (1/2)(AB + BC + CD + DA) < AC + BD < AB + BC + CD + DA

Chúc bạn học tốt !!!

                                  

Giả sử tứ giác ABCD có: AB=a,BC=b,CD=c,DA=d.

Gọi O là giao điểm của AC và BD ta có:

AC+BD=AO+OB+OC+OD>AB+CD=a+c

Tương tự: AC+BD>b+d.

Suy ra: 2(AC+BD)>a+b+c+d⇒AC+BD=a+b+c+d2

Vậy tổng hai đường chéo lớn hơn nửa chu vi của tứ giác.

Theo bất đẳng thức tam giác ta có:

AC<a+b;AC<c+d

BD<b+c;BD<a+d

⇒2(AC+BD)<2(a+b+c+d).

⇒AC+BD<a+b+c+d.

Vậy tổng hai dường chéo nhỏ hơn chu vi tứ giác.

Vo Trong Duy mang hình avata hentai

                       Giải:

Giả sử tứ giác ABCD có: AB=a,BC=b,CD=c,DA=d.
Gọi O là giao điểm của AC và BD ta có:
AC + BD = AO + OB + OC + OD > AB + CD = a + c
Tương tự: AC + BD > b + d

=> 2 ( AC + BD ) > a + b + c + d => AC + BD = a + b + c + d2

Vậy tổng hai đường chéo lớn hơn nửa chu vi của tứ giác.

Theo bất đẳng thức tam giác ta có như sau:

AC < a + b ; AC < c + d

BD < b + c ; BD < a + d

=>2(AC+BD)<2(a+b+c+d).

=>AC+BD<a+b+c+d.

Vậy tổng hai dường chéo nhỏ hơn chu vi tứ giác.

Học tốt

*YOUTUBER*

hoa hậu,k nha

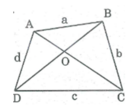
Đặt độ dài a = AB, b = BC, c = CD, d = AD

Gọi O là giao điểm 2 đường chéo AC và BD.

* Trong ∆ OAB, ta có:

OA + OB > a (bất đẳng thức tam giác) (1)

* Trong  ∆ OCD, ta có:

OC + OD > c (bất đẳng thức tam giác) (2)

Từ (1) và (2) suy ra:

OA + OB + OC + OD > a + c hay AC + BD > a + c (*)

* Trong  ∆ ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)

* Trong  ∆ OBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)

Từ (3) và (4) suy ra:

OA + OB + OC + OD > b + d hay AC + BD > b + d (**)

Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d

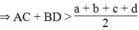
* Trong  ∆ ABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)

* Trong  ∆ ADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)

Suy ra: 2AC < a + b + c + d

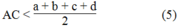
* Trong  ∆ ABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)

* Trong  ∆ BCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)

Suy ra: 2BD < a + b + c + d

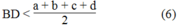
Từ (5) và (6) suy ra: AC + BD < a + b + c + d

bn vào phần câu hỏi tương tự nhé, trong đó có đấy

Đặt độ dài a = AB, b = BC, c = CD, d = AD

Gọi O là giao điểm 2 đường chéo AC và BD.

* Trong ΔOAB, ta có:

OA + OB > a (bất đẳng thức tam giác) (1)

* Trong ΔOCD, ta có:

OC + OD > c (bất đẳng thức tam giác) (2)

Từ (1) và (2) suy ra:

OA + OB + OC + OD > a + c hay AC + BD > a + c (*)

* Trong ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)

* Trong ΔOBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)

Từ (3) và (4) suy ra:

OA + OB + OC + OD > b + d hay AC + BD > b + d (**)

Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d

* Trong ΔABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)

* Trong ΔADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)

Suy ra: 2AC < a + b + c + d

* Trong ΔABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)

* Trong ΔBCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)

Suy ra: 2BD < a + b + c + d

Từ (5) và (6) suy ra: AC + BD < a + b + c + d

ĐÂY LÀ TOÁN LỚP 8 MÀ BẠN