Cho hình thang ABCD (AB//CD) có B=850 vậy số đo góc ngoài của đỉnh C
Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.

Vì AD vuông góc với hai đáy AB và CD nên \(\widehat{A}=\widehat{D}=90^0\)
Vì ABCD có 2 đáy AB,CD nên AB // CD. Do đó, \(\widehat B + \widehat C = 180^\circ \) ( 2 góc trong cùng phía)
Mặt khác:
\(\begin{array}{l}\widehat B = 2.\widehat C\\ \Rightarrow 2.\widehat C + \widehat C = 180^\circ \\ \Rightarrow 3.\widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ :3 = 60^\circ \end{array}\)
\(\Rightarrow \widehat B = 2. \widehat{C}=2.60^0=120^0\)
Vậy \(\widehat{A}=\widehat{D}=90^0; \widehat B = 120^0; \widehat C =60^0\)
Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các đường phân giác của góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Tính độ dài MN theo a, b, c, d (a. b, c, d có cùng đơn vị đo)
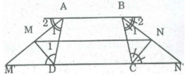
MN = (AB + M’N') / 2 (tính chất đường trung hình hình thang)
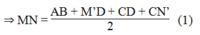
Mà M'D = AD, CN' = BC.
Thay vào (1) : ![]()
hình thang ABCD có AB // CD,AB=a,BC=b,CD=c,DA=d.các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cát nhau tại N
a.CMR MN//CD
b.Tính độ dài MN theo a,b,c,d(a,b,c,d có cùng đơn vị đo)
hình thang ABCD có AB//CD ,AB=a ,BC=b,CD=c,DA=d .Các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M , các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N
a) chứng minh rằng MN //CD
b) tính độ dài MN theo a,b,c,d (a,b,c,d có cùng đơn vị đo )
Hình thang ABCD có AB // CD, AB = a, BC = b, CD = c, DA = d. Các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N
a) Chứng minh rằng MN // CD
b) Tính độ dài MN theo a, b, c, d (a, b, c, d có cùng đơn vị đo)
xet tam giac ADM có
gocDAM=1/2 goc ngoai tai A
gocADM=1/2goc ngoai tai D
cong lai:gocADM+gocDAM=90*=> tam giac ADM vuông tại M
tương tự tam giac BNC vuông tại N
keo dai AM va` BN cắt CD tại E,F
xet tam giac ADE co DM vừa la` đường cao vừa la` phân giác => tam giac ADE can tai D=>DM la` trung tuyến =>M la` trung điểm AE
tương tự N la` trung diem BF
=> MN la` đuơng trung binh cua hinh thang AEFB =>MN//CD
Hình thang ABCD có AB // CD, AB = a, BC = b, CD = c, DA = d. Các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N.
a) Chứng minh MN // CD
b) Tính độ dài MN theo a, b, c, d ( a, b, c, d có cùng đơn vị đo )
Cho hình thang ABCD (AB // CD). Các đường phân giác của các góc ngoài tại đỉnh A và B cắt nhau ở M. Các đường phân giác của các góc ngoài tại đỉnh D và C. CMR:
a, MN // CD
b, Tính chu vi của hình thang ABCD biết MN = 4cm
hình thang ABCD có AB//CD ,AB=a,BC=b,CẢ=c,ĐÃ=d. các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M , các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N.
a, CMR MN//CD
b, tính độ dài MN theo a,b,c,đ [a,b,c,d có cùng đơn vị đo]
Hình thang ABCD có AB // CD; AB = a, BC = b, CD = c, DA = d. Các đường phân giác của góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N. Chứng minh rằng MN // CD
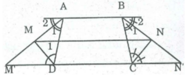
Gọi M' và N' là giao điểm của tia AM và BN với CD.
Ta có: ∠ (M') = ∠ A 2 (sole trong)
∠ A 1 = ∠ A 2 (gt)
⇒ ∠ (M') = ∠ A 1 nên ∆ ADM' cân tại D
* DM là phân giác của ∠ (ADM' )
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM'
∠ (N') = ∠ B 1 nên ∆ BCN' cân tại C.
* CN là phân giác của ∠ (BCN')
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN'
Suy ra: MN là đường trung bình của hình thang ABN'M'
⇒ MN // M'N' (tính chất đường trung hình hình thang)
Hay MN//CD
Hình thang ABCD, AB//CD có A - D = 2lần góc B = 2 lần gics C .Vậy số đo của AB bằng bao nhiêu?