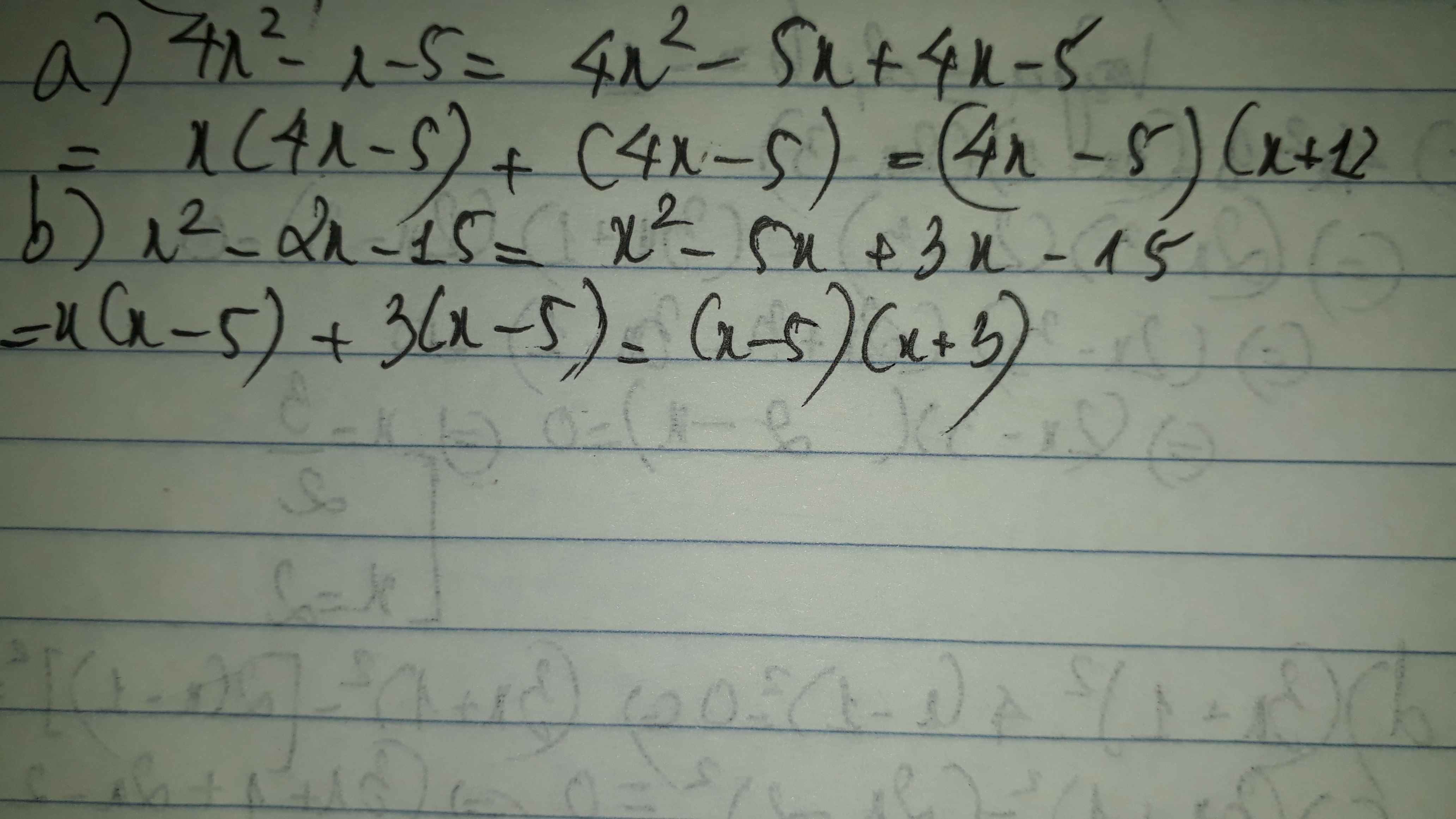Phân tích các đa thức sau thành nhân tử. Đáp án+ cách giải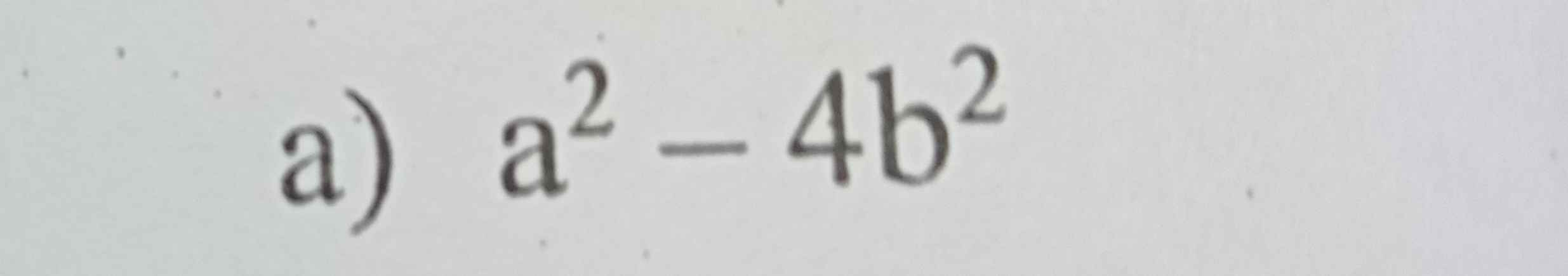

Những câu hỏi liên quan
Phân tích các đa thức sau thành nhân tử. Lời giải+ đáp án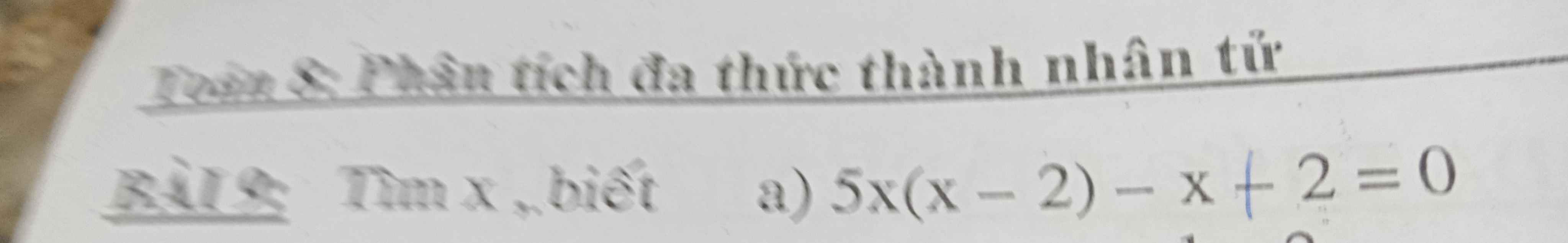
\(5x\left(x-2\right)-x+2=0\)
\(\Rightarrow5x\left(x-2\right)-\left(x-2\right)=0\)
\(\Rightarrow\left(5x-1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}5x-1=0\\x-2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=2\end{matrix}\right.\)
Vậy x=1/5 hoặc x=2
Đúng 0
Bình luận (0)
a: Ta có: \(5x\left(x-2\right)-x+2=0\)
\(\Leftrightarrow\left(x-2\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
phân tích các đa thức thành nhân tử
x2-4x-y2+4
mình cần đáp án chi tiết
\(x^2-4x-y^2+4=\left(x^2-4x+4\right)-y^2=\left(x-2\right)^2-y^2=\left(x-2-y\right)\left(x-2+y\right)\)
Đúng 1
Bình luận (1)
\(3x^2-3y^2-2\left(x-y\right)^2.\)
PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
( GHI CHI TIẾT LỜI GIẢI, KHÔNG GHI CHỈ ĐÁP ÁN )
\(3x^2-3y^2-2\left(x-y\right)^2\)
\(=3x^2-3y^2-2\left(x^2-2xy+y^2\right)\)
\(=3x^2-3y^2-2x^2+4xy-2y^2\)
\(=x^2+4xy-5y^2\)
\(=x^2+4xy+4y^2-9y^2\)
\(=\left(x+2y\right)^2-\left(3y\right)^2\)
\(=\left(x+2y-3y\right)\left(x+2y+3y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử: x^3+y^3+z^3-3xyz tui cần đáp án gấp ai trả lời được thì cho tui thanks?
phân tích đa thức thành nhân tử
cần đáp án chi tiết
x2-2x-3
\(x^2-2x-3=x^2-3x+x-3=x\left(x-3\right)+\left(x-3\right)=\left(x+1\right)\left(x-3\right)\)
Đúng 0
Bình luận (2)
2x2y+xy2-xy giúp mik ạ phân tích các đa thức sau thành phân tử bằng cách đặt nhân tử chung![]()
=xy*2x+xy*y-xy*1
=xy(2x+y-1)
Đúng 0
Bình luận (0)
Các bạn ơi giải hộ mình vs mình cần gấp:
phân tích các đa thức sau thành nhân tử:
X^3-2x^2-x+2
X^2+6x-y^2+9
Phân tích đa thức 2x^3y-2xy^3-4xy^2-2xy thành nhân tử
a) x3-2x2-x+2
=x(x2-1)+2(-x2+1)
=x(x2-1)-2(x2-1)
=(x2-1)(x-2)
b)
x2+6x-y2+9
=x2+6x+9-y2
=(x+3)2-y2
=(x+3-y)(x+3+y)
Đúng 1
Bình luận (0)
bài 1: Phân tích đa thức sau thành nhân tử ( làm bằng 2 cách: nhóm các hạng tử, tách hạng tử )
a,4x2 - x - 5
b,x2 - 2x - 15
a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)
b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)
Đúng 0
Bình luận (0)
Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:
\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)
Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?
`a^2 + ab + 2a + 2b = a(a+2) + b(a+2) = (a+b)(a+2)`
Đúng 1
Bình luận (0)