Đặt phép chia sau đo tính số dư

Vì x⁴+1 chia hết cho x²+ax +b ∀ x

⇒ số dư = 0 ⇒ từng cái = 0 ⇒ a= ; b =

\(\left(x^2-x+1\right)^2=x^4+x^2+1-2x^3+2x^2-2x=x^4-2x^3+3x^2-2x+1\)

Vậy a = -2; b = 1.

G

Câu hỏi của Khánh Ngọc Cute - Toán lớp 8 | Học trực tuyến

làm ơn giúp mình bài toán hình phần d với cảm ơn nhiều( hình lớp 7 đó)

Ta có:\(A=x^4-2x^3-x^2+ax+b\)

          \(A=x^3\left(x-2\right)-x\left(x-a\right)+b\)

                   Để A là đa thức thì x - a = x -2

                            Do đó a=2;b=0

Ta có:A=x4−2x3−x2+ax+b

          A=x3(x−2)−x(x−a)+b

                   Để A là đa thức thì x - a = x -2

                            Do đó a=2;b=0

\(A=x^4-2x^3-x^2+ax+b\)

 \(A=x^3\left(x-2\right)-x\left(x-a\right)+bA\)

\(x-a=x-2\)

\(=>a=2;b=0\)

~ Hok tốt ~

Đa thức dư là – x + 1 có hệ số tự do là 1.

Đáp án cần chọn là: C

\(A=5x^2y-xy^2+4xy+6\)             bậc : 3

a)\(B=-5x^2y+xy^2-4xy-6\)

b)\(=>C=-2xy+1-5x^2y+xy^2-4xy-6\)

\(C=-5x^2y+xy^2-6xy-5\)

A là đa thức có hệ số cao nhất là 1

=> A là bình phương của đa thức: \(\left(x^2+cx+d\right)^2\)

Ta có:\(\left(x^2+cx+d\right)^2=x^4+2cx^3+\left(2d+c^2\right)x^2+2cdx+d^2\)

=> \(x^4-2x^3+ax+b=x^4+2cx^3+\left(2d+c^2\right)x^2+2cdx+d^2\)

Cân bằng hệ số hai vế ta có:

\(2c=-2;2d+c^2=0;2cd=a;d^2=b\)

<=> \(c=-1;d=-\frac{1}{2};a=1;b=\frac{1}{4}\)

Vậy : \(A=x^4-2x^3+x+\frac{1}{4}=\left(x^2-x-\frac{1}{2}\right)^2\)

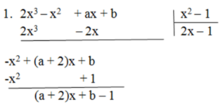
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0

Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1